Эта задача разбита на две. В данной задаче, вам нужно найти минимальный ответ. В задаче же Посёлок (Максимум) вам нужно найти максимальный возможный ответ. За каждую из этих задач можно получить по $$$50$$$ баллов.
В одном посёлке люди живут в $$$N$$$ домах. В каждом доме живёт ровно один житель. Дома соединены дорогами. Каждая дорога соединяет два дома и имеет длину $$$1$$$ км. Из каждого дома можно достичь любой другой дом, идя по одной или нескольким дорогам. В общем в посёлке ровно $$$N-1$$$ дорог.
Однажды все жители решили переехать в другие дома. После переезда всех жителей в каждом доме снова должен жить ровно один житель, но ни один житель не должен остаться в том же доме, в котором жил до этого. Наша цель — узнать наименьшую возможную сумму кратчайших путей (в км) перемещения всех жителей из старых мест жительства на новые.
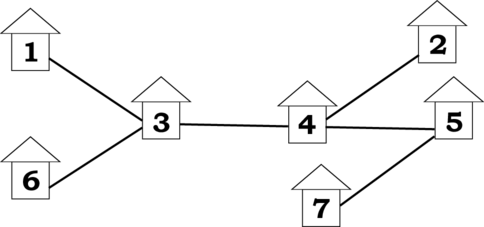
Пример посёлка с семью домами
Например, если всего есть семь домов, соединённых дорогами так, как показано на рисунке, то наименьшая общая длина равняется $$$8$$$ км (этого можно достичь, перемещая жителей $$$1 \to 6$$$, $$$2 \to 4$$$, $$$3 \to 1$$$, $$$4 \to 2$$$, $$$5 \to 7$$$, $$$6 \to 3$$$, $$$7 \to 5$$$).
Напишите программу, которая находит наименьшую возможную сумму кратчайших путей (в км), а также распределение жителей по новым домам.
Первая строка содержит одно целое число $$$N$$$ ($$$1 < N \le 10^5$$$). Дома пронумерованы последовательными целыми числами $$$1, 2, \ldots, N$$$.
Затем следуют $$$N-1$$$ строк, которые описывают дороги. Каждая строка содержит два целых числа $$$a$$$ и $$$b$$$ ($$$1 \le a, b \le N$$$, $$$a \neq b$$$), что означает, что дома с номерами $$$a$$$ и $$$b$$$ соединены дорогой.
В первой строке выведите одно целое число, наименьшую возможную общую длину кратчайших путей жителей в километрах.
Во второй строке опишите одно правильное распределение жителей по новым домам с наименьшей возможной общей длиной: $$$N$$$ различных целых чисел $$$v_1, v_2, \ldots, v_N$$$. Для каждого $$$i$$$, $$$v_i$$$ обозначает номер дома, в который должен переехать житель из дома с номером $$$i$$$ ($$$v_i \neq i$$$). Если существует несколько распределений, выведите любое из них.
Подзадачи:
- (6 баллов) $$$N \leq 10$$$
- (19 баллов) $$$N \leq 1\,000$$$
- (25 баллов) Без дополнительных ограничений.
4 1 2 2 3 3 4
4 2 1 4 3
7 4 2 5 7 3 4 6 3 1 3 4 5
8 3 4 6 2 7 1 5
| Название |
|---|




