| Codeforces Round 663 (Div. 2) |
|---|
| Закончено |
У вас есть простой связный неориентированный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер.
Рассмотрим все способы разбить на пары некоторое подмножество из этих $$$n$$$ вершин, чтобы ни одна вершина не присутствовала более чем в одной паре.
Такое паросочетание считается хорошим, если для каждой пары выбранных пар индуцированный подграф, содержащий все $$$4$$$ вершины, по два из каждой пары, имеет не более $$$2$$$ ребер (из $$$6$$$ возможных ребер). Более формально, для любых двух выбранных пар $$$(a,b)$$$ и $$$(c,d)$$$ индуцированный подграф с вершинами $$$\{a,b,c,d\}$$$ должен иметь не более $$$2$$$ ребер.
Обратите внимание, что подграф, индуцированный набором вершин, содержит вершины только из этого набора и ребра, оба конца которых находятся в этом наборе.
Теперь сделайте одно из двух
- Найдите простой путь, состоящий как минимум из $$$\lceil \frac{n}{2} \rceil$$$ вершин. Здесь путь называется простым, если он не посещает какую-либо вершину несколько раз.
- Найдите хорошее паросочетание, в котором по крайней мере у $$$\lceil \frac{n}{2} \rceil$$$ вершин есть пара.
Можно показать, что в каждом графе, удовлетворяющим ограничениям из условия, можно найти или первое, или второе (или оба).
Каждый тест содержит несколько наборов входных данных. В первой строке записано количество наборов входных данных $$$t$$$ ($$$1 \le t \le 10^5$$$). Описание наборов входных данных приведено ниже.
Первая строка каждого набора входных данных содержит $$$2$$$ целых числа $$$n, m$$$ ($$$2 \le n \le 5\cdot 10^5$$$, $$$1 \le m \le 10^6$$$), обозначающих количество вершин и ребер графа соответственно.
Каждая из следующих $$$m$$$ строк содержит $$$2$$$ целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$), что обозначает наличие неориентированного ребра между вершинами $$$u$$$ и $$$v$$$ в данном графе.
Гарантируется, что данный граф является связным и простым — он не содержит кратных ребер и петель.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$5\cdot 10^5$$$.
Гарантируется, что сумма $$$m$$$ по всем наборам входных данных не превышает $$$10^6$$$.
Для каждого набора входных данных придерживайтесь следующего формата вывода:
Если вы нашли хорошее паросочетание, в первой строке выведите «PAIRING» (без кавычек).
- Затем выведите $$$k$$$ ($$$\lceil \frac{n}{2} \rceil \le 2\cdot k \le n$$$), количество пар в вашем паросочетании.
- Затем в каждой из следующих $$$k$$$ строк выведите по $$$2$$$ целых числа $$$a$$$ и $$$b$$$ —, обозначающих, что $$$a$$$ и $$$b$$$ находятся в одной паре. Заметьте, что в графе не обязано быть ребро между вершинами $$$a$$$ и $$$b$$$!
- Это паросочетание должно быть хорошим, и каждая вершина должен входить не более в $$$1$$$ пару.
В противном случае в первой строке выведите «PATH» (без кавычек).
- Затем выведите $$$k$$$ ($$$\lceil \frac{n}{2} \rceil \le k \le n$$$), количество узлов на вашем пути.
- Затем во второй строке выведите $$$k$$$ целых чисел, $$$v_1, v_2, \ldots, v_k$$$, в том порядке, в котором они встречаются на пути. Формально, $$$v_i$$$ и $$$v_{i+1}$$$ должны иметь ребро между ними для каждого $$$i$$$ ($$$1 \le i < k$$$).
- Этот путь должен быть простым, то есть ни одна вершина не должна встречаться на нем более одного раза.
4 6 5 1 4 2 5 3 6 1 5 3 5 6 5 1 4 2 5 3 6 1 5 3 5 12 14 1 2 2 3 3 4 4 1 1 5 1 12 2 6 2 7 3 8 3 9 4 10 4 11 2 4 1 3 12 14 1 2 2 3 3 4 4 1 1 5 1 12 2 6 2 7 3 8 3 9 4 10 4 11 2 4 1 3
PATH 4 1 5 3 6 PAIRING 2 1 6 2 4 PAIRING 3 1 8 2 5 4 10 PAIRING 4 1 7 2 9 3 11 4 5
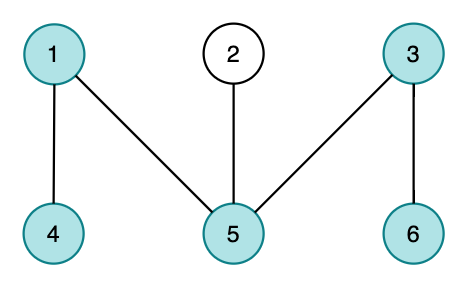
Путь, полученный в первом наборе входных данных, следующий.
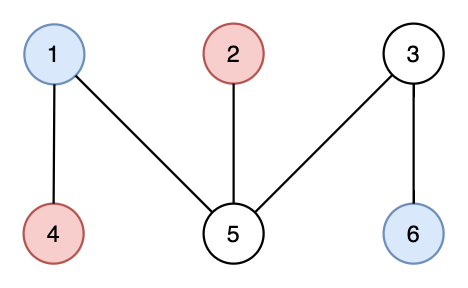
Вот хорошее паросочетание для первого набора входных данных.
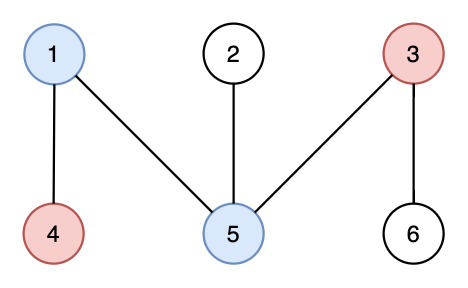
Вот нехорошее паросочетание для первого набора входных данных — подграф $$$\{1,3,4,5\}$$$ имеет $$$3$$$ ребра.
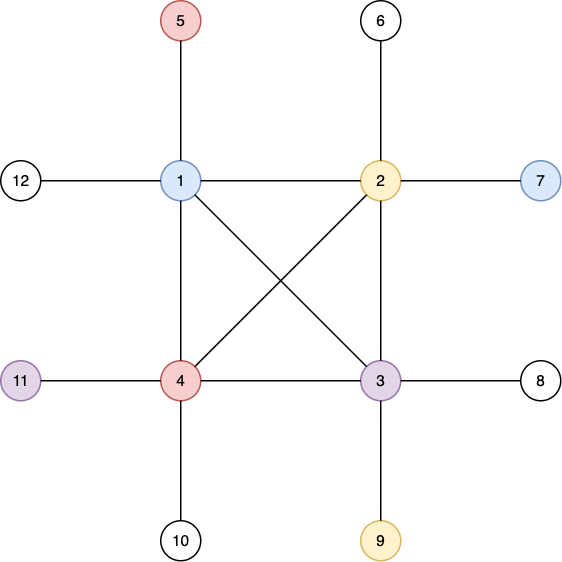
Вот паросочетание, полученное во втором наборе входных данных.
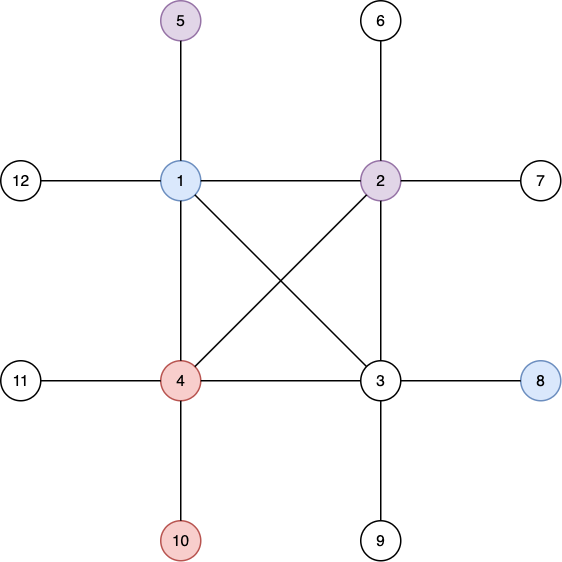
Оно хорошее потому, что —
- Подграф $$$\{1,8,2,5\}$$$ содержит ребра ($$$1$$$,$$$2$$$) и ($$$1$$$,$$$5$$$).
- Подграф $$$\{1,8,4,10\}$$$ содержит ребра ($$$1$$$,$$$4$$$) и ($$$4$$$,$$$10$$$).
- Подграф $$$\{4,10,2,5\}$$$ содержит ребра ($$$2$$$,$$$4$$$) и ($$$4$$$,$$$10$$$).
Вот еще одно хорошее паросочетание для второго набора входных данных.
| Название |
|---|




