| Grakn Forces 2020 |
|---|
| Закончено |
Вам дано $$$m$$$ множеств $$$A_1, A_2, \ldots, A_m$$$, состоящих из целых чисел; элементы этих множеств — целые числа от $$$1$$$ до $$$n$$$ включительно.
Есть два массива положительных целых чисел $$$a_1, a_2, \ldots, a_m$$$ и $$$b_1, b_2, \ldots, b_n$$$.
За одну операцию вы можете удалить элемент $$$j$$$ из множества $$$A_i$$$ и заплатить за это $$$a_i + b_j$$$ монет.
Вы можете сделать несколько (возможно, ноль) операций (после этого некоторые множества могут стать пустыми).
После этого вы построите неориентированный граф, где каждое ребро будет иметь цвет. Граф будет иметь $$$n$$$ вершин. Для каждого множества $$$A_i$$$ вы добавите ребро $$$(x, y)$$$ цвета $$$i$$$ для всех $$$x, y \in A_i$$$ и $$$x < y$$$. Некоторые пары вершин могут быть соединены больше чем одним ребром, но такие ребра будут иметь разные цвета.
Мы называем цикл $$$i_1 \to e_1 \to i_2 \to e_2 \to \ldots \to i_k \to e_k \to i_1$$$ ($$$e_j$$$ это какое-то ребро, соединяющее вершины $$$i_j$$$ и $$$i_{j+1}$$$ этого графа) разноцветным, если цвета всех ребер этого цикла различны.
Найдите минимальное количество монет, которое нужно заплатить, чтобы получить граф без разноцветных циклов.
В первой строке находится два целых числа $$$m$$$ и $$$n$$$ ($$$1 \leq m, n \leq 10^5$$$), количество множеств и количество вершин в графе.
Во второй строке находятся $$$m$$$ целых чисел $$$a_1, a_2, \ldots, a_m$$$ ($$$1 \leq a_i \leq 10^9$$$).
В третьей строке находятся $$$n$$$ целых чисел $$$b_1, b_2, \ldots, b_n$$$ ($$$1 \leq b_i \leq 10^9$$$).
В каждой из следующих $$$m$$$ строк находится описание множества. В $$$i$$$-й строке первое число $$$s_i$$$ ($$$1 \leq s_i \leq n$$$) равно размеру $$$A_i$$$. Затем следуют $$$s_i$$$ целых чисел — элементы множества $$$A_i$$$. Эти целые числа различны и находятся в пределах от $$$1$$$ до $$$n$$$ включительно.
Гарантируется, что сумма $$$s_i$$$ для всех $$$1 \leq i \leq m$$$ не превосходит $$$2 \cdot 10^5$$$.
Выведите единственное целое число — минимальное количество монет, которое нужно заплатить, чтобы получить граф без разноцветных циклов.
3 2 1 2 3 4 5 2 1 2 2 1 2 2 1 2
11
7 8 3 6 7 9 10 7 239 8 1 9 7 10 2 6 239 3 2 1 3 2 4 1 3 1 3 7 2 4 3 5 3 4 5 6 7 2 5 7 1 8
66
В первом тесте можно сделать следующие операции.
- Удалить элемент $$$1$$$ из множества $$$1$$$. Вы должны заплатить $$$a_1 + b_1 = 5$$$ монет за эту операцию.
- Удалить элемент $$$1$$$ из множества $$$2$$$. Вы должны заплатить $$$a_2 + b_1 = 6$$$ монет за эту операцию.
Суммарно вы заплатите $$$11$$$ монет. После этих операций первое и второй множества будут равны $$$\{2\}$$$, а третье множество будет равно $$$\{1, 2\}$$$. Поэтому построенный граф будет содержать одно ребро $$$(1, 2)$$$ цвета $$$3$$$.
Во втором тесте можно сделать следующие операции.
- Удалить элемент $$$1$$$ из множества $$$1$$$. Вы должны заплатить $$$a_1 + b_1 = 11$$$ монет за эту операцию.
- Удалить элемент $$$4$$$ из множества $$$2$$$. Вы должны заплатить $$$a_2 + b_4 = 13$$$ монет за эту операцию.
- Удалить элемент $$$7$$$ из множества $$$3$$$. Вы должны заплатить $$$a_3 + b_7 = 13$$$ монет за эту операцию.
- Удалить элемент $$$4$$$ из множества $$$4$$$. Вы должны заплатить $$$a_4 + b_4 = 16$$$ монет за эту операцию.
- Удалить элемент $$$7$$$ из множества $$$6$$$. Вы должны заплатить $$$a_6 + b_7 = 13$$$ монет за эту операцию.
Суммарно вы заплатите $$$66$$$ монет. После этих операций будут следующие множества:
- $$$\{2, 3\}$$$;
- $$$\{1\}$$$;
- $$$\{1, 3\}$$$;
- $$$\{3\}$$$;
- $$$\{3, 4, 5, 6, 7\}$$$;
- $$$\{5\}$$$;
- $$$\{8\}$$$.
Вы построите такой граф:
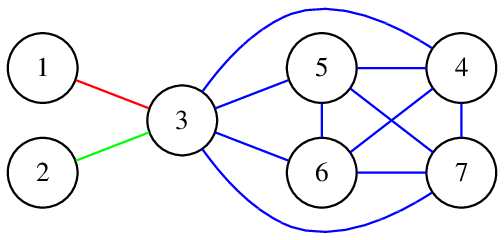
В нем нет разноцветных циклов.
| Название |
|---|




