На выставке змей есть $$$n$$$ комнат (пронумерованных от $$$0$$$ до $$$n - 1$$$) расположенных по кругу. В каждой комнате находится одна змея. Комнаты соединены $$$n$$$ конвейерами, $$$i$$$-й из них соединяет комнаты $$$i$$$ и $$$(i+1) \bmod n$$$. Другими словами, комнаты $$$0$$$ и $$$1$$$, $$$1$$$ и $$$2$$$, $$$\ldots$$$, $$$n-2$$$ и $$$n-1$$$, $$$n-1$$$ и $$$0$$$ соединены конвейерами.
Конвейер $$$i$$$ может быть в одном из трех состояний:
- Если он направлен по часовой стрелке, змеи могут проползти только из комнаты $$$i$$$ в $$$(i+1) \bmod n$$$.
- Если он направлен против часовой стрелки, змеи могут пройти только из комнаты $$$(i+1) \bmod n$$$ в $$$i$$$.
- Если он выключен, змеи могут проползти в обоих направлениях.
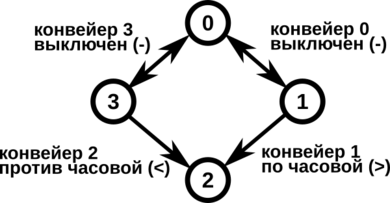
В этом примере $$$4$$$ комнаты, где конвейеры $$$0$$$ и $$$3$$$ выключены, конвейер $$$1$$$ направлен по часовой стрелке, а конвейер $$$2$$$ — против часовой стрелки.
Каждая змея хочет покинуть свою комнату, поползать и вернуться в нее потом снова. Назовем комнату возвратимой, если змея может покинуть ее и вернуться в нее позже, ползая по конвейерам. Сколько всего возвратимых комнат?
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится единственное целое число $$$t$$$ ($$$1 \le t \le 1000$$$): количество наборов входных данных. Описание наборов входных данных следует.
В первой строке описания каждого набора входных данных находится единственное целое число $$$n$$$ ($$$2 \le n \le 300\,000$$$): количество комнат.
В следующей строке описания каждого набора входных данных находится строка $$$s$$$ длины $$$n$$$, состоящая только из символов «<», «>» и «-».
- Если $$$s_{i} = $$$ «>», то $$$i$$$-й конвейер направлен по часовой стрелке.
- Если $$$s_{i} = $$$ «<», то $$$i$$$-й конвейер направлен против часовой стрелки.
- Если $$$s_{i} = $$$ «-», то $$$i$$$-й конвейер выключен.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$300\,000$$$.
Для каждого набора входных данных выведите количество возвратимых комнат.
4 4 -><- 5 >>>>> 3 <-- 2 <>
3 5 3 0
В первом наборе входных данных все комнаты являются возвратимыми, кроме комнаты $$$2$$$. Змея в комнате $$$2$$$ заблокирована и не может выйти. Этот набор входных данных соответствует картинке из условия задачи.
Во втором наборе входных данных все комнаты являются возвратимыми, потому что можно вернуться в любую комнату, несколько раз пройдя по конвейерам, направленным по часовой стрелке.
| Название |
|---|




