| Codeforces Round 103 (Div. 2) |
|---|
| Закончено |
Побочной диагональю квадратной матрицы называется диагональ, проходящая из правого верхнего угла матрицы в левый нижний угол. Назовем лесенкой порядка n квадратную матрицу n × n без клеток выше побочной диагонали (ниже на рисунке изображена лесенка пятого порядка).
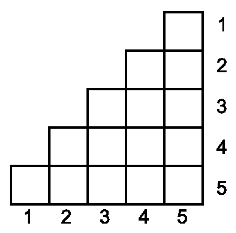
В клетках лесенки порядка n стоят m спортсменов.
За секунду спортсмен может перейти на соседнюю по стороне клетку лесенки. Перед началом соревнования каждый спортсмен должен выбрать один из кратчайших путей до побочной диагонали.
После стартового свистка соревнование начинается, и все спортсмены начинают двигаться по выбранным путям. Когда спортсмен достигает клетки побочной диагонали, он останавливается и больше не двигается. Соревнование заканчивается, когда все спортсмены доходят до побочной диагонали. Соревнование считается успешным, если в процессе соревнования никакие два спортсмена не оказались одновременно в одной клетке (в том числе в одной клетке побочной диагонали не может остановиться более одного спортсмена). Если один спортсмен в данный момент времени уходит из клетки, а другой приходит в нее, то считается, что они не оказались в одной клетке одновременно. Заметим, что другие крайние случаи (например, если спортсмены идут навстречу друг другу) исключаются, так как выбранные пути кратчайшие.
Даны позиции m спортсменов на лесенке. Требуется выбрать из них наибольшее количество спортсменов (все невыбранные спортсмены удаляются из клеток лесенки до начала движения), так чтобы для них соревнование могло бы быть успешным (то есть существовал такой выбор кратчайших путей для спортсменов, при котором в процессе соревнования никакие два спортсмена не оказались бы одновременно в одной клетке).
В первой строке заданы два целых числа n и m (1 ≤ n, m ≤ 105). Далее в m строках заданы координаты спортсменов на лесенке парами чисел ri, ci (1 ≤ ri, ci ≤ n, n - ci < ri), где ri — номер строки лесенки, ci — номер столбца лесенки (для понимания того как нумеруются строки и столбцы смотрите поясняющие рисунки). Никакие два спортсмена не стоят в одной клетке лесенки.
В первую строку выведите количество выбранных спортсменов. Во вторую строку выведите номера выбранных спортсменов в любом порядке, разделяя числа пробелами. Если ответов несколько разрешается вывести любой. Спортсмены нумеруются начиная с единицы в том порядке, в котором они заданы во входных данных.
3 3
2 3
3 2
3 3
3
1 2 3
Пояснение к первому примеру.
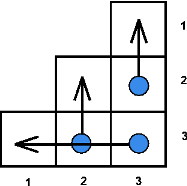
| Название |
|---|




