Дано дерево, в котором каждая вершина покрашена в белый, чёрный или серый цвета. К дереву можно применять операцию удаления — выбрать множество вершин, находящихся в одной компоненте связности, и удалить эти вершины со смежными рёбрами из графа. Единственное ограничение — нельзя выбирать множество, в котором одновременно есть и белая, и чёрная вершины.
Нужно удалить из графа все вершины за минимальное количество операций удаления.
Каждый тест содержит несколько наборов входных данных. В первой строке содержится целое число $$$t$$$ ($$$1 \le t \le 100\,000$$$) — количество наборов входных данных в тесте.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$1 \le n \le 200\,000$$$) — количество вершин в дереве.
Вторая строка каждого набора входных данных содержит $$$n$$$ целых чисел $$$a_v$$$ ($$$0 \le a_v \le 2$$$) — цвета вершин в дереве. Серые вершины имеют $$$a_v=0$$$, белые вершины имеют $$$a_v=1$$$, чёрные вершины имеют $$$a_v=2$$$.
Следующие $$$n-1$$$ строк каждого набора входных данных содержат пары чисел $$$u, v$$$ ($$$1 \le u, v \le n$$$) — рёбра дерева.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превысит $$$200\,000$$$.
Для каждого набора входных данных выведите одно целое число — минимальное количество операций.
4 2 1 1 1 2 4 1 2 1 2 1 2 2 3 3 4 5 1 1 0 1 2 1 2 2 3 3 4 3 5 8 1 2 1 2 2 2 1 2 1 3 2 3 3 4 4 5 5 6 5 7 5 8
1 3 2 3

В первом тесте обе вершины имеют белый цвет, и их можно удалить одной операцией.

Во втором тесте можно применить три операции: сначала удалить обе чёрные вершины, 2 и 4, а после этого за две операции по отдельности удалить вершины 1 и 3. За одну операцию этого не сделать, потому что после удаления вершины 2 они оказались в разных компонентах связности.
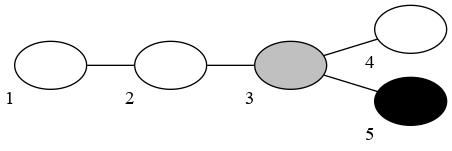
В третьем тесте можно первой операцией удалить вершины 1, 2, 3, 4 — среди них три белых и одна серая, а после этого одной операцией удалить последнюю вершину — 5.
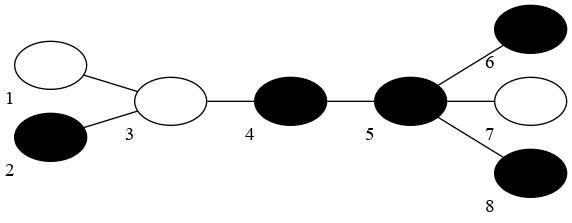
В четвёртом тесте достаточно трёх операций. Один из вариантов, как это можно сделать, — удалить сразу все чёрные вершины, второй операцией удалить белую вершину 7, а последней операцией удалить связные белые вершины 1 и 3.
| Название |
|---|




