На координатной плоскости была нарисована замкнутая ломаная, состоящая из вертикальных и горизонтальных отрезков (параллельных осям координат). Горизонтальные и вертикальные отрезки этой ломаной чередовались (за горизонтальным отрезком шёл вертикальный, и наоборот). В этой ломаной не было пересечений отрезков по внутренним точкам, то есть если какие-то два отрезка пересекались, то точка их пересечения являлась одним из концом каждого из них (обратите внимание на примеры в пояснении к условию).
К сожалению, ломаную стёрли, а про неё осталось совсем немного информации: известны лишь длины всех вертикальных и всех горизонтальных отрезков. Вам требуется восстановить любую ломаную, удовлетворяющую условию, или определить, что такой ломаной не существует.
В первой строке задано целое число $$$t$$$ ($$$1 \leq t \leq 200$$$) — количество наборов входных данных.
В первой строке каждого набора входных данных задано одно целое число $$$h$$$ ($$$1 \leq h \leq 1000$$$) — количество горизонтальных отрезков.
Во второй строке каждого набора заданы $$$h$$$ целых чисел $$$l_1, l_2, \dots, l_h$$$ ($$$1 \leq l_i \leq 1000$$$) — длины горизонтальных отрезков ломаной, в произвольном порядке.
В третьей строке задано одно целое число $$$v$$$ ($$$1 \leq v \leq 1000$$$) — количество вертикальных отрезков.
В четвёртой строке заданы $$$v$$$ целых чисел $$$p_1, p_2, \dots, p_v$$$ ($$$1 \leq p_i \leq 1000$$$) — длины вертикальных отрезков ломаной, в произвольном порядке.
Все наборы входных данных разделяются пустой строкой.
Сумма $$$h + v$$$ по всем наборам входных данных не превосходит $$$1000$$$.
Для каждого набора входных данных выведите слово Yes, если требуемая ломаная существует или No в противном случае. Если ломаная существует, в следующих $$$n$$$ строках выведите последовательно вершины этой ломаной. В $$$i$$$-й строке выведите два целых числа $$$x_i$$$, $$$y_i$$$ — координаты $$$i$$$-й вершины.
Обратите внимание, что все отрезки этой ломаной должны быть параллельны осям координат, при этом после горизонтального отрезка должен идти вертикальный, и наоборот. Все координаты не должны превосходить $$$10^9$$$ по абсолютной величине.
2 2 1 1 2 1 1 2 1 2 2 3 3
Yes 1 0 1 1 0 1 0 0 No
2 4 1 1 1 1 4 1 1 1 1 3 2 1 1 3 2 1 1
Yes 1 0 1 1 2 1 2 2 1 2 1 1 0 1 0 0 Yes 0 -2 2 -2 2 -1 1 -1 1 0 0 0
2 4 1 4 1 2 4 3 4 5 12 4 1 2 3 6 2 1 3
Yes 2 0 2 3 3 3 3 7 4 7 4 12 0 12 0 0 No
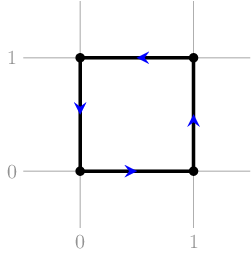
В первом наборе первого примера ответ Yes — в качестве примера можно привести квадрат:
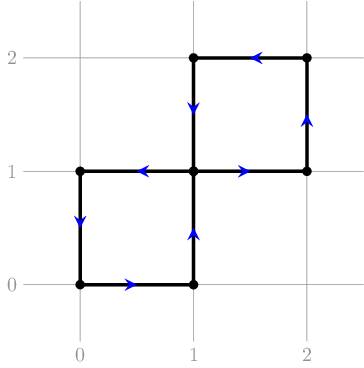
В первом наборе второго примера искомая ломаная существует. Обратите внимание, что ломаная пересекается по вершинам-концам отрезков:
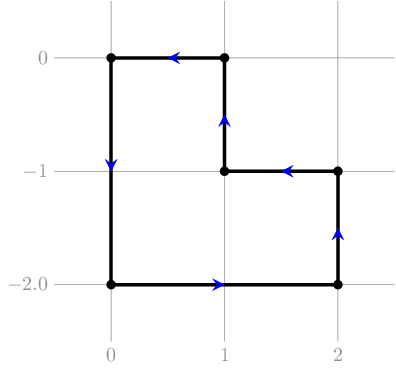
Во втором наборе второго примера искомая ломаная может выглядеть, как на рисунке ниже:
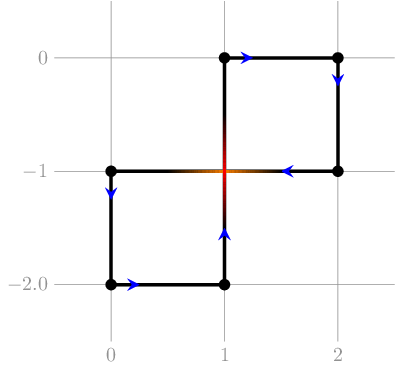
Обратите внимание, что пример ниже не будет корректным для этого набора входных данных, так как содержит самопересечения:
| Название |
|---|




