Для заданной последовательности попарно различных неотрицательных целых чисел $$$(b_1, b_2, \dots, b_k)$$$ мы определяем, является ли она хорошей следующим образом:

• Рассмотрим граф на $$$k$$$ вершинах, на которых написаны числа от $$$b_1$$$ до $$$b_k$$$.
• Для каждого $$$i$$$ от $$$1$$$ до $$$k$$$ мы находим такое $$$j$$$ ($$$1 \le j \le k$$$, $$$j\neq i$$$), для которого значение $$$(b_i \oplus b_j)$$$ минимально среди всех таких $$$j$$$, где $$$\oplus$$$ обозначает операцию побитового исключающего ИЛИ. После этого мы проводим неориентированное ребро между вершинами с числами $$$b_i$$$ и $$$b_j$$$.
• Последовательность называется хорошей, если и только если получившийся граф является деревом (то есть он связан и не имеет простых циклов).

Возможно, что для некоторых чисел $$$b_i$$$ и $$$b_j$$$ вы попробуете добавить ребро между ними дважды. Тем не менее вы добавите это ребро только один раз.

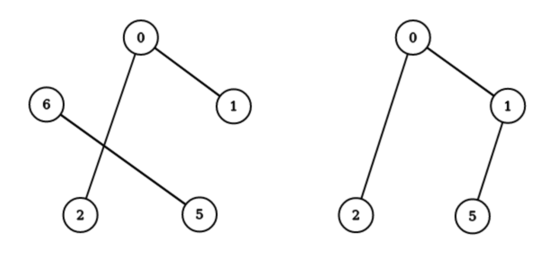
Ниже приведен пример (рисунок, соответствующий первому примеру).

Последовательность $$$(0, 1, 5, 2, 6)$$$ не хорошая, так как мы не можем достичь $$$1$$$ из $$$5$$$.

Однако, последовательность $$$(0, 1, 5, 2)$$$ является хорошей.

Вам дана последовательность $$$(a_1, a_2, \dots, a_n)$$$ из попарно различных неотрицательных целых чисел. Вы хотите удалить из нее некоторые элементы (возможно, ни одного), чтобы сделать оставшуюся последовательность хорошей. Какое минимально возможное количество удалений необходимо для достижения этой цели?

Можно показать, что для любой последовательности можно удалить некоторое количество элементов, оставив как минимум $$$2$$$, так, что оставшаяся последовательность будет хорошей.