| Codeforces Global Round 12 |
|---|
| Закончено |
Единственное различие между простой и сложной версиями задачи состоит в том, что символ O не встречается во входных данных простой версии.
Errichto бросил Monogon-у следующий вызов, чтобы запугать его и не дать занять первое место по вкладу на Codeforces.
В таблице для игры в крестики нолики есть $$$n$$$ строк и $$$n$$$ столбцов. Каждая клетка таблицы либо пустая, либо содержит фишку. Всего есть два типа фишек: X и O. Если есть три фишки одного типа, последовательные в какой-то строке или в каком-то столбце, то это выигрышная конфигурация. Иначе это ничейная конфигурация.
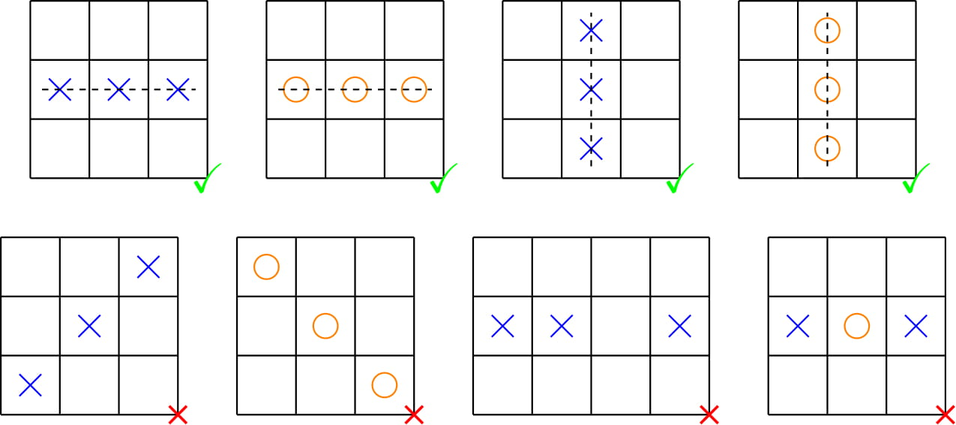 Примеры в первой строке это выигрышные конфигурации. Примеры во второй строке это ничейные конфигурации.
Примеры в первой строке это выигрышные конфигурации. Примеры во второй строке это ничейные конфигурации. За одну операцию вы можете поменять фишку X на O или фишку O на X. Обозначим за $$$k$$$ общее количество фишек в таблице. Ваша задача сделать таблицу ничейной за не более $$$\lfloor \frac{k}{3}\rfloor$$$ (округление вниз) операций.
Вы не обязаны минимизировать количество операций.
В первой строке находится единственное целое число $$$t$$$ ($$$1\le t\le 100$$$) — количество наборов входных данных.
В первой строке описания каждого набора входных данных находится единственное целое число $$$n$$$ ($$$1\le n\le 300$$$) — размер таблицы.
В следующих $$$n$$$ строках находятся строки, состоящие из $$$n$$$ символов, задающие изначальную таблицу. Символ в $$$i$$$-й строке и $$$j$$$-м столбце это '.', если клетка пустая, иначе он совпадает с типом фишки, содержащейся в этой клетке таблицы: 'X' или 'O'.
Гарантируется, что не все клетки пустые.
Сумма $$$n$$$ по всем наборам входных данных не превосходит $$$300$$$.
Для каждого набора входных данных выведите состояние таблицы после выполнения операций.
У нас есть доказательство, что решение всегда существует. Если есть несколько возможных решений, выведите любое.
3 3 .O. OOO .O. 6 XXXOOO XXXOOO XX..OO OO..XX OOOXXX OOOXXX 5 .OOO. OXXXO OXXXO OXXXO .OOO.
.O. OXO .O. OXXOOX XOXOXO XX..OO OO..XX OXOXOX XOOXXO .OXO. OOXXO XXOXX OXXOO .OXO.
В первом наборе входных данных есть изначально три 'O' последовательных во второй строке и во втором столбце. Изменив фишку посередине на 'X' мы получим ничейную конфигурацию. При этом мы поменяли $$$1\le \lfloor 5/3\rfloor$$$ фишку.
Во втором наборе входных данных итоговая конфигурация ничейная. Мы поменяли $$$8\le \lfloor 32/3\rfloor$$$ фишек.
В третьем наборе входных данных итоговая конфигурация ничейная. Мы поменяли $$$7\le \lfloor 21/3\rfloor$$$ фишек.
| Название |
|---|




