| Codeforces Global Round 12 |
|---|
| Закончено |
Единственное различие между двумя версиями задачи состоит в том, что в простой версии задачи нет обновлений.
Есть $$$n$$$ катушек, расположенных вокруг круглого стола. Катушки бывают двух цветов: черного и белого.
Любые две катушки одного цвета можно соединить нитью-отрезком того же цвета. Определим соответствие как способ соединить катушки так, что каждая катушка будет соединена ровно с одной другой катушкой.
Раскраска это выбор цветов (белого или черного) для каждой катушки. Раскраска называется возможной, если для нее существует хотя бы одно соответствие. Это равносильно тому, что количества черных и белых катушек четные.
Для соответствия можно посчитать количество раз, которое какая-то белая нить пересекает какую-то черную нить. Мы считаем не количество точек пересечения, а количество пар нитей разных цветов, которые пересекаются, поэтому одна точка пересечения может быть посчитана несколько раз, если несколько пар нитей пересекаются в одной и той же точке. Если $$$c$$$ это возможная раскраска, обозначим за $$$f(c)$$$ минимальное количество пересечений по всем возможным корректным соответствиям для этой раскраски.
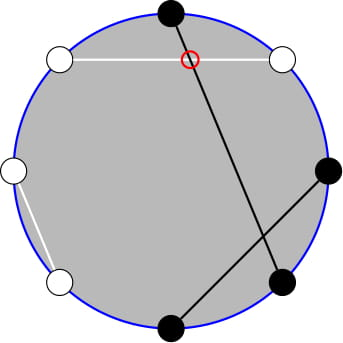 Картинка изображает раскраску bwbbbwww. Для нарисованного соответствия есть одно пересечение между нитями разного цвета. Можно показать, что это минимальное возможное количество по всем корректным соответствиям для этой раскраски, поэтому $$$f(\text{bwbbbwww}) = 1$$$.
Картинка изображает раскраску bwbbbwww. Для нарисованного соответствия есть одно пересечение между нитями разного цвета. Можно показать, что это минимальное возможное количество по всем корректным соответствиям для этой раскраски, поэтому $$$f(\text{bwbbbwww}) = 1$$$. Вам дана строка $$$s$$$ описывающая незавершенную раскраску с черными, белыми и непокрашенными катушками. Раскраска $$$c$$$ называется $$$s$$$-достижимой, если ее можно получить, раскрасив все непокрашенные катушки в $$$s$$$, не меняя цвета остальных.
Раскраска $$$c$$$ выбирается случайно равновероятно по всем возможным $$$s$$$-достижимым раскраскам. Найдите математическое ожидание $$$f(c)$$$. Вы должны найти его по модулю $$$998244353$$$.
Также будет производиться $$$m$$$ изменений одного символа в $$$s$$$. После каждого изменения вы должны посчитать математическое ожидание $$$f(c)$$$ снова.
Можно показать, что каждый ответ может быть записан в виде $$$\frac{p}{q}$$$, где $$$p$$$ и $$$q$$$ некоторые взаимно простые целые числа и $$$q\not\equiv 0\pmod{998244353}$$$. Тогда ответ по модулю $$$998244353$$$ будет равен $$$(p\cdot q^{-1})$$$ modulo $$$998244353$$$.
В первой строке находится два целых числа $$$n$$$, $$$m$$$ ($$$2\le n\le 2\cdot 10^5$$$, $$$n$$$ четное, $$$0\le m\le 2\cdot 10^5$$$) — количество катушек и изменений, соответственно.
Во второй строке находится строка $$$s$$$ длины $$$n$$$ — незавершенная раскраска катушек. $$$i$$$-й символ будет 'w', 'b' или '?', и будет описывать цвет $$$i$$$-й катушки как белый, черный и непокрашенный, соответственно.
Каждая из следующих $$$m$$$ строк содержит целое число $$$i$$$ ($$$1 \leq i \leq n$$$) — позицию символа в $$$s$$$, который будет изменен и символ $$$c$$$ ($$$c \in \{\text{w}, \text{b}, \text{?}\}$$$) — новый цвет катушки $$$i$$$ после изменения.
Гарантируется, что существует хотя бы одна непокрашенная катушка изначально и после каждого изменения.
Выведите $$$m+1$$$ строку: математическое ожидание $$$f(c)$$$ изначально и после каждого изменения. Все значения должны быть найдены по модулю $$$998244353$$$.
8 0 bwbb?www
1
10 3 ???ww?wb?? 4 ? 5 ? 2 w
436731905 218365953 374341633 530317313
4 3 bw?b 1 w 2 b 1 w
0 0 1 1
Первый тест почти соответствует картинке. Нельзя покрасить '?' в 'w', потому что тогда получится не возможная раскраска, потому что количество черных катушек будет нечетным. Тогда единственная достижимая возможная раскраска это 'bwbbbwww'. Поскольку $$$f(\text{bwbbbwww}) = 1$$$ математическое ожидание равно $$$1$$$.
Во втором тесте строка после каждого изменения будет:
- ????w?wb??
- ??????wb??
- ?w????wb??
В третьем тесте строка после каждого изменения будет:
- ww?b
- wb?b
- wb?b
| Название |
|---|




