Вам заданы четыре различные целые точки $$$p_1$$$, $$$p_2$$$, $$$p_3$$$ и $$$p_4$$$ на коодинатной плоскости $$$\mathit{XY}$$$.
За один шаг вы можете выбрать одну из точек $$$p_i$$$ и сдвинуть ее в одном из четырех направлений на единицу. Другими словами, если вы выбрали точку $$$p_i = (x, y)$$$, вы можете передвинуть ее в $$$(x, y + 1)$$$, $$$(x, y - 1)$$$, $$$(x + 1, y)$$$ или $$$(x - 1, y)$$$.
Ваша задача — сдвинуть точки таким образом, чтобы они образовали квадрат со сторонами параллельными осям $$$\mathit{OX}$$$ и $$$\mathit{OY}$$$ (квадрат со стороной $$$0$$$ разрешен).
Какое минимальное количество шагов вам нужно, чтобы получить такой квадрат?
В первой строке задано единственное целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Каждый набор состоит из четырех строк. В каждой строке заданы два целых числа $$$x$$$ и $$$y$$$ ($$$0 \le x, y \le 10^9$$$) — координаты одной из точек $$$p_i = (x, y)$$$.
Все точки в одном наборе различные.
Для каждого набора входных данных, выведите единственное число — минимальное количество шагов, необходимых для получения квадрата.
3 0 2 4 2 2 0 2 4 1 0 2 0 4 0 6 0 1 6 2 2 2 5 4 1
8 7 5
В первом наборе входных данных, один из оптимальных ответов изображен ниже:
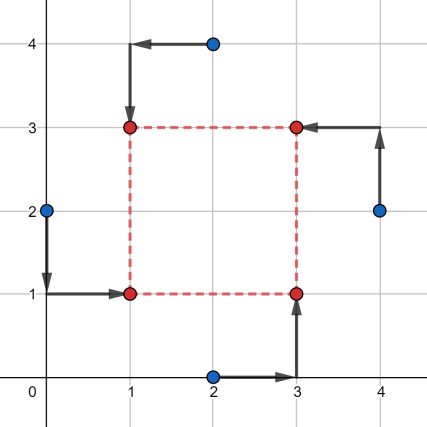
Во втором наборе, один из оптимальных ответов изображен ниже:
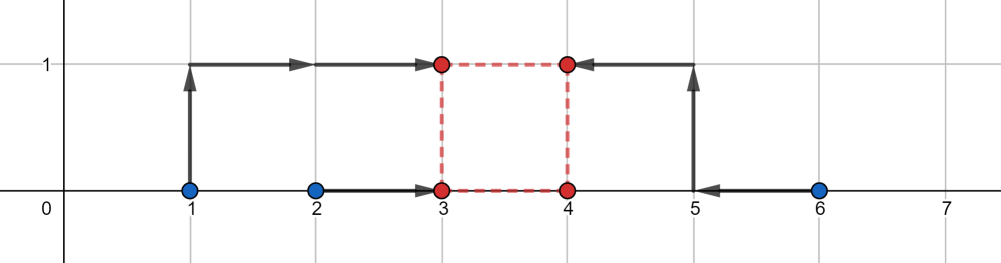
В третьем наборе, один из оптимальных ответов изображен ниже:
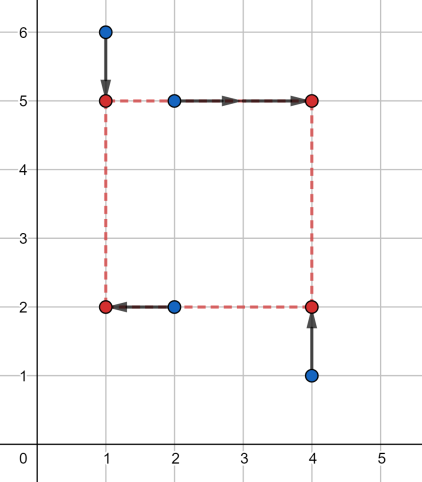
| Название |
|---|




