// Мы решили не давать легенду про розетки, но вы все еще можете придумать ее сами :^)
Определим цепь:
- цепь длины $$$1$$$ — это одна вершина;
- цепь длины $$$x$$$ — это цепь длины $$$x-1$$$ с одной вершиной, присоединенной к ее концу одним ребром.
Даны $$$n$$$ цепей длин $$$l_1, l_2, \dots, l_n$$$. Вы хотите построить дерево, используя некоторые из них.
- Каждая вершина дерево либо белая, либо черная.
- Изначально дерево содержит только одну вершину, которая является корневой и белой.
- Изначально все цепи содержат только белые вершины.
- Вы можете взять одну из цепей и соединить любую ее вершину с любой белой вершиной дерева ребром. Цепь становится частью дерева. Оба конца ребра становятся черными.
- Каждая цепь может быть использована не более одного раза.
- Некоторые цепи можно оставить неиспользованными.
Расстояние между двумя вершинами в дереве равно количеству ребер на кратчайшем пути между ними.
Если в полученном дереве есть хотя бы $$$k$$$ белых вершин, то его значение равно расстоянию от корня до $$$k$$$-й ближайшей белой вершины.
Какое минимальное значение может иметь полученное дерево? Если не существует способа построить дерева с хотя бы $$$k$$$ белыми вершинами, то выведите -1.
В первой строке записаны два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$2 \le k \le 10^9$$$) — количество цепей и минимальное количество белых вершин, которые должно иметь дерево.
Во второй строке записаны $$$n$$$ целых чисел $$$l_1, l_2, \dots, l_n$$$ ($$$3 \le l_i \le 2 \cdot 10^5$$$) — длины цепей.
Выведите одно целое число. Если не существует способа построить дерева с хотя бы $$$k$$$ белыми вершинами, то выведите -1. В противном случае выведите минимальное значение, которое может иметь дерево.
1 2 3
2
3 3 4 3 3
3
3 5 4 3 4
4
2 10 5 7
-1
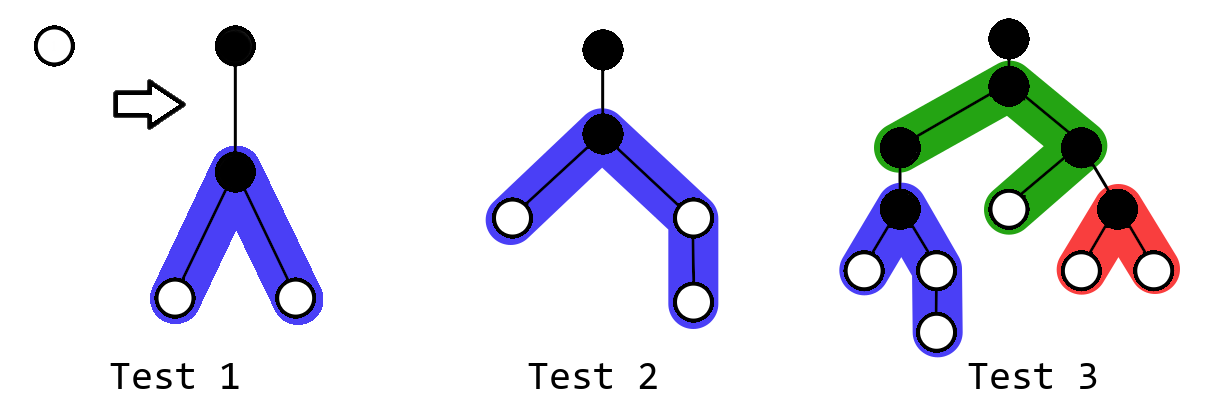
Разрешается использовать не все цепи, поэтому оптимальное использовать только цепь длины $$$4$$$ во втором примере.
| Название |
|---|




