Рассмотрим дорогу, состоящую из нескольких рядов. Каждый ряд разделен на несколько прямоугольных плиток, и все плитки в одном ряду одинаковы. Первый ряд содержит ровно одну прямоугольную плитку. Посмотрите на рисунок ниже, который показывает, как расположены плитки.
Дорога построена следующим образом:
- первый ряд состоит из $$$1$$$ плитки;
- затем следует $$$a_1$$$ рядов; каждый из этих рядов содержит на $$$1$$$ плитку больше, чем предыдущий ряд;
- затем следует $$$b_1$$$ рядов; каждый из этих рядов содержит на $$$1$$$ плитку меньше, чем предыдущий ряд;
- затем следует $$$a_2$$$ рядов; каждый из этих рядов содержит на $$$1$$$ плитку больше, чем предыдущий ряд;
- затем следует $$$b_2$$$ рядов; каждый из этих рядов содержит на $$$1$$$ плитку меньше, чем предыдущий ряд;
- ...
- затем следует $$$a_n$$$ рядов; каждый из этих рядов содержит на $$$1$$$ плитку больше, чем предыдущий ряд;
- затем следует $$$b_n$$$ рядов; каждый из этих рядов содержит на $$$1$$$ плитку меньше, чем предыдущий ряд;
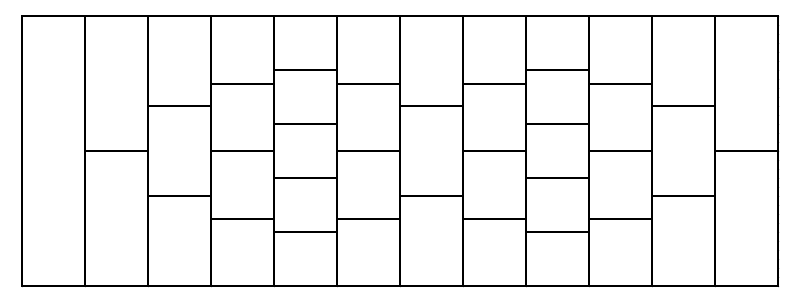Пример дороги с $$$n = 2$$$, $$$a_1 = 4$$$, $$$b_1 = 2$$$, $$$a_2 = 2$$$, $$$b_2 = 3$$$. Ряды расположены слева направо. Вы начинаете с единственной плитки в первом ряду и хотите добраться до последнего ряда (любой плитки из нее). От вашей текущей плитки вы можете перейти к любой плитке в следующем ряду, которая касается с вашей текущей плиткой.
Вычислите количество различных путей от первого ряда до последнего. Поскольку оно может быть большим, выведите его по модулю $$$998244353$$$.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 1000$$$).
Затем следует $$$n$$$ строк. $$$i$$$-я из них содержит два целых числа $$$a_i$$$ и $$$b_i$$$ ($$$1 \le a_i, b_i \le 10^5$$$; $$$|a_i - b_i| \le 5$$$).
Дополнительное ограничение: последовательность $$$a_i$$$ и $$$b_i$$$ никогда не приводит к ряду с неположительным числом плиток.
Выведите одно целое число — количество путей от первого ряда до последнего, взятое по модулю $$$998244353$$$.
2 4 2 2 3
850
3 4 1 2 3 3 1
10150
8 328 323 867 868 715 718 721 722 439 435 868 870 834 834 797 796
759099319
