У вас есть $$$n$$$ цепей, и $$$i$$$-я цепь состоит из $$$c_i$$$ вершин. Вершины в каждой цепи пронумерованы независимо от $$$1$$$ по $$$c_i$$$ вдоль этой цепи. Другими словами, $$$i$$$-я цепь — это неориентированный граф из $$$c_i$$$ вершин и $$$(c_i - 1)$$$ ребер, соединяющих $$$j$$$-ю и $$$(j + 1)$$$-ю вершины для всех $$$1 \le j < c_i$$$.
Вы решили объединить эти цепи в один граф следующим образом:
- первая цепь пропускается;
- $$$1$$$-я вершина $$$i$$$-й цепи соединяется ребром с $$$a_i$$$-й вершиной $$$(i - 1)$$$-й цепи;
- последняя ($$$c_i$$$-я) вершина $$$i$$$-й цепи соединяется ребром с $$$b_i$$$-й вершиной $$$(i - 1)$$$-й цепи.
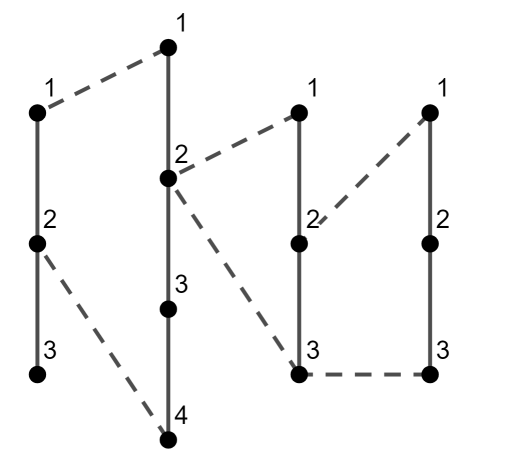 Изображение первого набора входных данных. Пунктирные линии означают ребра, добавленные во время объединения
Изображение первого набора входных данных. Пунктирные линии означают ребра, добавленные во время объединения Посчитайте длину наидлиннейшего простого цикла в полученном графе.
Простой цикл — это, фактически, цепь, в которой первая и последняя вершины также соединены ребром. Если двигаться вдоль простого цикла, то мы посетим каждую вершину этого цикла ровно по одному разу.
В первой строке задано одно целое число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных.
В первой строке каждого набора задано одно целое число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество цепей.
Во второй строке каждого набора заданы $$$n$$$ целых чисел $$$c_1, c_2, \dots, c_n$$$ ($$$2 \le c_i \le 10^9$$$) — количество вершин в соответствующих цепях.
В третьей строке каждого набора заданы $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$a_1 = -1$$$; $$$1 \le a_i \le c_{i - 1}$$$).
В четвертой строке каждого наборе заданы $$$n$$$ целых чисел $$$b_1, b_2, \dots, b_n$$$ ($$$b_1 = -1$$$; $$$1 \le b_i \le c_{i - 1}$$$).
Оба числа $$$a_1$$$ и $$$b_1$$$ равны $$$-1$$$, они не используются в построении графа и заданы лишь для соответствия нумерации. Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных, выведите длину наибольшего простого цикла.
3 4 3 4 3 3 -1 1 2 2 -1 2 2 3 2 5 6 -1 5 -1 1 3 3 5 2 -1 1 1 -1 3 5
7 11 8
В первом наборе входных данных, наидлиннейший простой цикл изображен ниже:
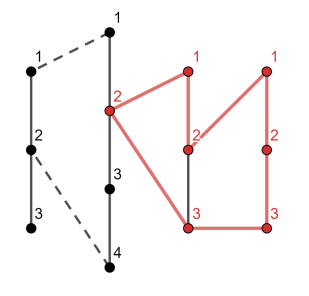
Мы не можем увеличить этот цикл с помощью первой цепи, так как в этом случае цикл уже не будет простым — вершина $$$2$$$ на второй цепи нарушит простоту цикла.
| Название |
|---|




