| Codeforces Round 698 (Div. 1) |
|---|
| Закончено |
Nezzar любит игру osu!.
osu! играется на карте, которая может быть представлена как массив различных точек на плоскости. Карта называется красивой, если для любых трех последовательных точек $$$A,B,C$$$, записанных в порядке следования в массиве, угол между этими тремя точками с центром в $$$B$$$ будет строго меньше, чем $$$90$$$ градусов.
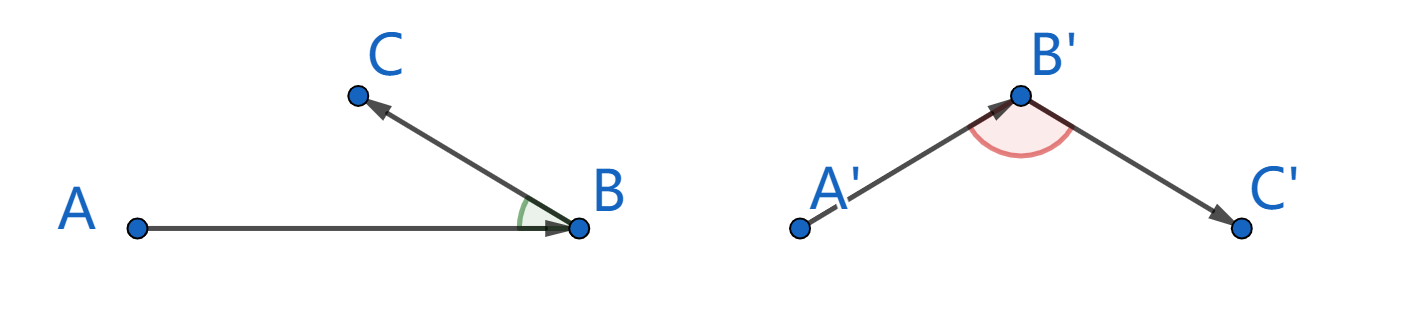 Точки $$$A,B,C$$$ слева образуют угол меньший, чем $$$90$$$ градусов, поэтому они могут быть тремя последовательными точками в красивой карте; точки $$$A',B',C'$$$ справа образуют угол, больший либо равный $$$90$$$ градусам, поэтому они не могут быть тремя последовательными точками в красивой карте.
Точки $$$A,B,C$$$ слева образуют угол меньший, чем $$$90$$$ градусов, поэтому они могут быть тремя последовательными точками в красивой карте; точки $$$A',B',C'$$$ справа образуют угол, больший либо равный $$$90$$$ градусам, поэтому они не могут быть тремя последовательными точками в красивой карте. Сейчас у Nezzar есть карта, состоящая из $$$n$$$ различных точек $$$A_1,A_2,\ldots,A_n$$$. Nezzar хочет переупорядочить эти $$$n$$$ точек так, чтобы получившаяся карта стала красивой.
Более формально, вы должны найти перестановку $$$p_1,p_2,\ldots,p_n$$$ целых чисел от $$$1$$$ до $$$n$$$ такую, что карта $$$A_{p_1},A_{p_2},\ldots,A_{p_n}$$$ будет красивой. Если это невозможно, вы должны определить это.
В первой строке находится единственное целое число $$$n$$$ ($$$3 \le n \le 5000$$$).
Затем следуют $$$n$$$ строк, в $$$i$$$-й из них находятся два целых числа $$$x_i$$$, $$$y_i$$$ ($$$-10^9 \le x_i, y_i \le 10^9$$$) — координаты точки $$$A_i$$$.
Гарантируется, что все точки различны.
Если решения нет, выведите $$$-1$$$.
Иначе выведите $$$n$$$ чисел, образующих допустимую перестановку $$$p$$$.
Если существует несколько возможных решений, вы можете вывести любое.
5 0 0 5 0 4 2 2 1 3 0
1 2 5 3 4
Это иллюстрация к первому примеру:
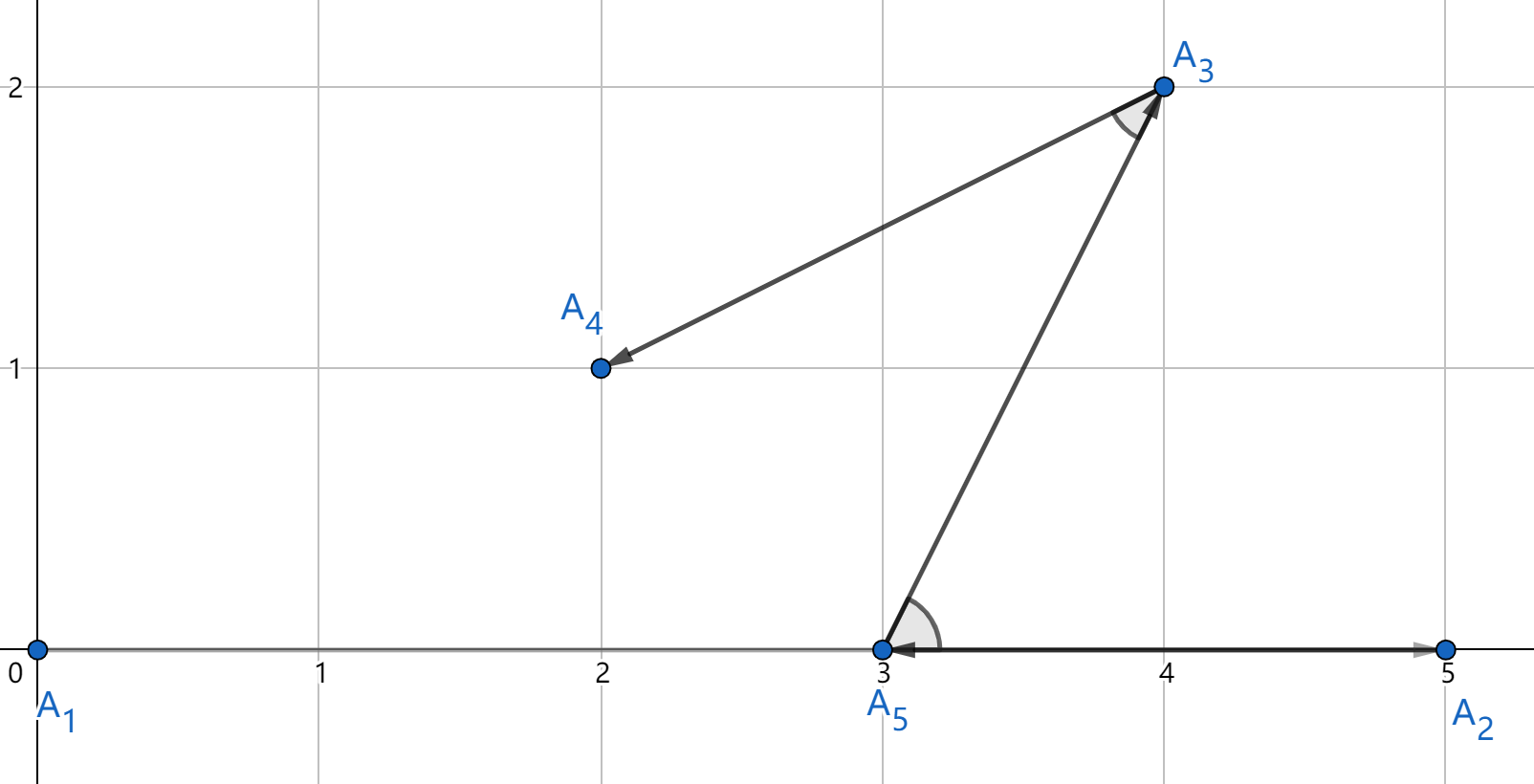
Обратите внимание, что угол между $$$A_1$$$, $$$A_2$$$ и $$$A_5$$$ с центром в $$$A_2$$$ равен $$$0$$$ градусов. Однако угол между $$$A_1$$$, $$$A_5$$$ и $$$A_2$$$ с центром в $$$A_5$$$ равен $$$180$$$ градусам.
| Название |
|---|




