| Codeforces Round 703 (Div. 2) |
|---|
| Закончено |
У вас есть дерево из $$$n$$$ вершин, а также $$$m$$$ простых вершинных путей. Ваша задача — найти, сколько пар этих путей пересекаются по ровно одной вершине. Более формально, вам нужно найти число пар $$$(i, j)$$$ $$$(1 \leq i < j \leq m)$$$ таких, что $$$path_i$$$ и $$$path_j$$$ имеют ровно одну общую вершину.
В первой строке находится единственное целое число $$$n$$$ $$$(1 \leq n \leq 3 \cdot 10^5)$$$.
Следующие $$$n - 1$$$ строк описывают дерево. На каждой строке находится два целых числа $$$u$$$ и $$$v$$$ $$$(1 \leq u, v \leq n)$$$ описывающие ребро между вершинами $$$u$$$ и $$$v$$$.
В следующей строке находится единственное целое число $$$m$$$ $$$(1 \leq m \leq 3 \cdot 10^5)$$$.
Следующие $$$m$$$ строк описывают пути. Каждая строка описывает путь своими крайними точками $$$u$$$ и $$$v$$$ $$$(1 \leq u, v \leq n)$$$. Путь задается всеми вершинами на кратчайшем пути из $$$u$$$ в $$$v$$$ (включая $$$u$$$ и $$$v$$$).
Выведите единственное целое число — количество пар путей, которые пересекаются по ровно одной вершине.
5 1 2 1 3 1 4 3 5 4 2 3 2 4 3 4 3 5
2
1 3 1 1 1 1 1 1
3
5 1 2 1 3 1 4 3 5 6 2 3 2 4 3 4 3 5 1 1 1 2
7
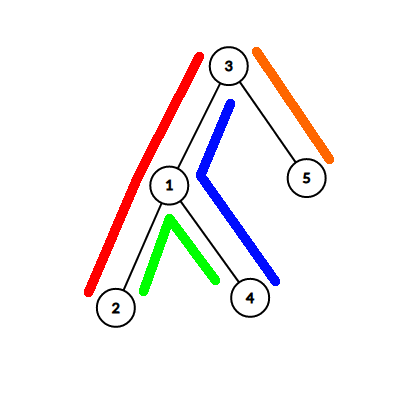
Дерево и пути в первом примере выглядят так. Пары $$$(1,4)$$$ и $$$(3,4)$$$ пересекаются по ровно одной вершине.
Во втором примере все пути состоят из единственной одинаковой вершины, так что все пары $$$(1, 2)$$$, $$$(1, 3)$$$ и $$$(2, 3)$$$ пересекаются по одной вершине.
Третий пример, такой же как первый, но с двумя дополнительными путями. Пары $$$(1,4)$$$, $$$(1,5)$$$, $$$(2,5)$$$, $$$(3,4)$$$, $$$(3,5)$$$, $$$(3,6)$$$ и $$$(5,6)$$$ пересекаются по ровно одной вершине.
| Название |
|---|




