| Codeforces Round 106 (Div. 2) |
|---|
| Закончено |
Петя очень любит футбол, особенно когда родителей нет дома. Каждое утро он выходит во двор, собирает своих друзей, и они играют вместе весь день, изредка прерываясь на еду или какие-нибудь важные дела (например, поливание цветов).
Самое главное в футболе — перед началом игры честно поделиться на команды. Во дворе в футбол играют n ребят (считая самого Петю), умение каждого мальчика играть в футбол выражается неотрицательной характеристикой ai (чем она больше, тем лучше мальчик играет).
Обозначим за x количество игроков в первой команде, y — количество игроков во второй команде, pi — номера ребят, вошедших в первую команду, qi — номера ребят, вошедших во вторую команду. Разделение n ребят на две команды считается честным, если выполнены три условия:
- Каждый мальчик играет ровно в одной команде (x + y = n).
- Размеры команд отличаются не более, чем на единицу (|x - y| ≤ 1).
- Суммарные умения играть в футбол у двух команд отличаются не более, чем на величину умения самого лучшего игрока во дворе. Более формально:
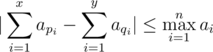
Ваша задача — помочь ребятам честно разделиться на две команды. Гарантируется, что честное разделение на две команды всегда существует.
В первой строке записано единственное целое число n (2 ≤ n ≤ 105) — количество ребят во дворе. В следующей строке записаны n целых положительных чисел, разделенных пробелами, ai (1 ≤ ai ≤ 104), i-е число обозначает умение играть i-го мальчика.
В первой строке выведите целое число x — количество мальчиков в первой команде, во второй строке выведите x целых чисел — номера мальчиков, попавших в первую команду. В третьей строке выведите целое число y — количество мальчиков во второй команде, в четвертой строке выведите y целых чисел — номера мальчиков, попавших во вторую команду. Не забудьте, что должны выполняться все три условия: x + y = n, |x - y| ≤ 1, а также условие на разницу суммарных умений.
Если решений несколько, выведите любое.
Мальчики нумеруются начиная с единицы в том порядке, в котором заданы их умения во входных данных. Номера мальчиков из одной команды разрешается выводить в любом порядке.
3
1 2 1
2
1 2
1
3
5
2 3 3 1 1
3
4 1 3
2
5 2
Рассмотрим первый тестовый пример. В нем мы берем первого и второго мальчика в первую команду, а третьего мальчика во вторую команду. Проверим все три условия честного разделения. Первое ограничение выполнено (все мальчики участвуют в игре), второе ограничение на размеры групп (|2 - 1| = 1 ≤ 1) выполнено, третье ограничение на разность умений ((2 + 1) - (1) = 2 ≤ 2) выполнено.
| Название |
|---|




