| Codeforces Round 706 (Div. 1) |
|---|
| Закончено |
«Добытчик алмазов» — игра, похожая на «Добытчик золота», но в этой игре $$$n$$$ шахтеров, а не $$$1$$$.
Шахта может быть представлена как плоскость. Будем рассматривать $$$n$$$ шахтеров как $$$n$$$ точек, расположенных на оси y. В шахте расположены $$$n$$$ алмазов, будем рассматривать их как $$$n$$$ точек на оси x. По каким-то причинам ни шахтеры, ни алмазы не могут быть расположены в начале координат (точке $$$(0, 0)$$$).
Каждый шахтер должен добыть ровно один алмаз. У каждого шахтера есть крюк, с помощью которого он может достать алмаз. Если шахтер, находящийся в точке $$$(a,b)$$$ использует свой крюк для добычи алмаза, расположенного в точке $$$(c,d)$$$, он потратит $$$\sqrt{(a-c)^2+(b-d)^2}$$$ (расстояние между точками) единиц энергии. Шахтеры не могут перемещаться и помогать друг другу.
Цель игры — распределить алмазы по шахтерам так, чтобы минимизировать сумму затраченной энергии. Сможете ли вы найти этот возможный минимум?
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1\le t\le 10$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
Первая строка каждого набора входных данных содержит единственное целое число $$$n$$$ ($$$1 \le n \le 10^5$$$) — количество шахтеров и алмазов.
Каждая из следующих $$$2n$$$ строк содержит два целых числа $$$x$$$ ($$$-10^8 \le x \le 10^8$$$) и $$$y$$$ ($$$-10^8 \le y \le 10^8$$$), описывающие некоторую точку $$$(x,y)$$$, в которой находится шахтер или алмаз. Гарантируется, что либо $$$x = 0$$$, что значит, что в точке $$$(0, y)$$$ находится шахтер, либо $$$y = 0$$$, что значит, что в точке $$$(x, 0)$$$ находится алмаз. В одной точке могут находится несколько шахтеров или алмазов.
Гарантируется, что никакая точка не находится в начале координат. Также гарантируется, что на оси x ровно $$$n$$$ точек, и на оси y тоже ровно $$$n$$$ точек.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите одно вещественное число — минимально возможную сумму затраченных энергий.
Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не превосходит $$$10^{-9}$$$.
Формально, пусть ваш ответ равен $$$a$$$, а ответ жюри равен $$$b$$$. Ваш ответ будет зачтен, если и только если $$$\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-9}$$$.
3 2 0 1 1 0 0 -1 -2 0 4 1 0 3 0 -5 0 6 0 0 3 0 1 0 2 0 4 5 3 0 0 4 0 -3 4 0 2 0 1 0 -3 0 0 -10 0 -2 0 -10
3.650281539872885 18.061819283610362 32.052255376143336
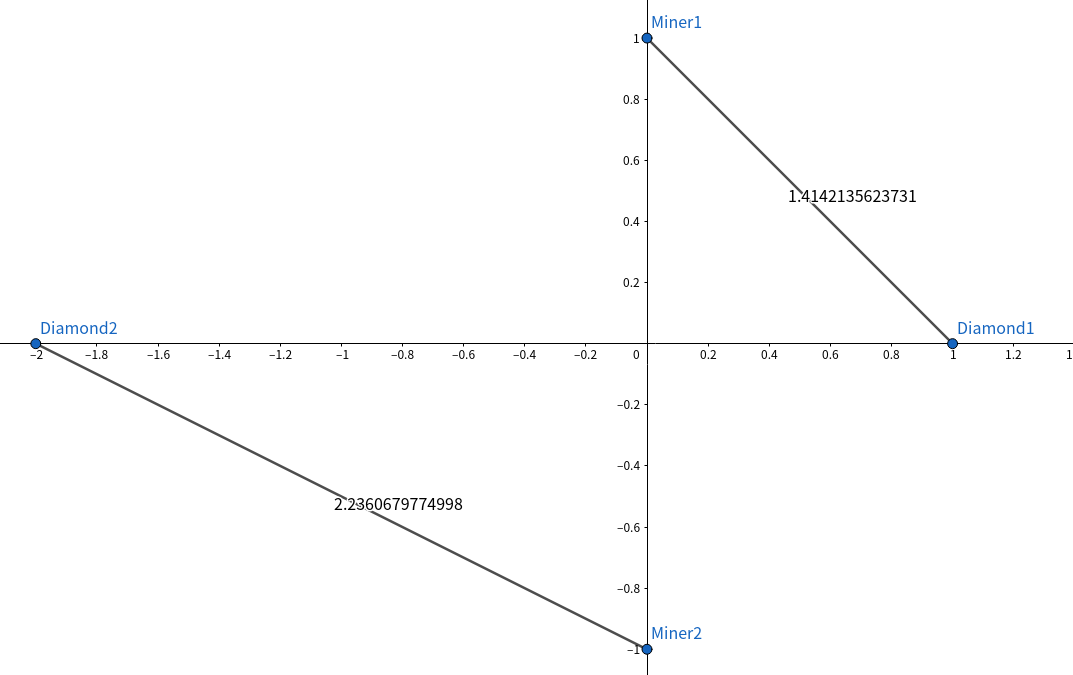
В первом примере есть два шахтера в точках $$$(0,1)$$$ и $$$(0,-1)$$$, а алмазы расположены в точках $$$(1,0)$$$ и $$$(-2,0)$$$. Если распределить алмазы по шахтерам, как показано на рисунке, то потратится $$$\sqrt2 + \sqrt5$$$ единиц энергии.
| Название |
|---|




