| Codeforces Round 706 (Div. 1) |
|---|
| Закончено |
$$$n$$$ квадратов нарисованы на полу слева направо. На $$$i$$$-м квадрате записаны три целых числа $$$p_i,a_i,b_i$$$. Последовательность $$$p_1,p_2,\dots,p_n$$$ образует перестановку.
Во время каждого раунда вы будете стартовать с самого левого квадрата $$$1$$$ и прыгать вправо. Если вы сейчас на $$$i$$$-м квадрате, вы можете сделать одну из следующих двух операций:
- Перепрыгнуть на $$$i+1$$$-й квадрат и заплатить за это $$$a_i$$$. Если $$$i=n$$$, тогда вы можете закончить раунд, заплатив $$$a_i$$$.
- Перепрыгнуть на $$$j$$$-й квадрат и заплатить за это $$$b_i$$$, где $$$j$$$ — это самый левый квадрат, который удовлетворяет условиям $$$j > i, p_j > p_i$$$. Если таких $$$j$$$ не существует, вы можете закончить раунд, заплатив $$$b_i$$$.
В игре будет $$$q$$$ раундов. Чтобы сделать ее сложнее, вы должны поддерживать множество квадратов $$$S$$$ (изначально пустое). Вы обязаны оказаться на этих квадратах во время раунда (вы можете также побывать и в других квадратах). Множество квадратов $$$S$$$ для $$$i$$$-го раунда получается добавлением или удалением одного квадрата из множества квадратов для $$$(i-1)$$$-го раунда.
Для каждого раунда найдите минимальную цену, которую вы должны заплатить, чтобы его закончить.
В первой строке находятся два целых числа $$$n$$$, $$$q$$$ ($$$1\le n,q\le 2 \cdot 10^5$$$) — количество квадратов и количество раундов.
Во второй строке находятся $$$n$$$ различных целых чисел $$$p_1,p_2,\dots,p_n$$$ ($$$1\le p_i\le n$$$). Гарантируется, что последовательность $$$p_1,p_2,\dots,p_n$$$ образует перестановку.
В третьей строке находятся $$$n$$$ целых чисел $$$a_1,a_2,\ldots,a_n$$$ ($$$-10^9\le a_i\le 10^9$$$).
В четвертой строке находятся $$$n$$$ целых чисел $$$b_1,b_2,\dots,b_n$$$ ($$$-10^9\le b_i\le 10^9$$$).
Затем следуют $$$q$$$ строк, $$$i$$$-я из них содержит единственное целое число $$$x_i$$$ ($$$1\le x_i\le n$$$). Если $$$x_i$$$ было в множестве $$$S$$$ для $$$(i-1)$$$-го раунда, то вы должны удалить его, иначе вы должны добавить его.
Выведите $$$q$$$ строк, каждая из них должна содержать единственное целое число — минимальную цену, которую вы должны заплатить, чтобы закончить соответствующий раунд.
3 2 2 1 3 10 -5 4 3 -2 3 1 2
6 8
5 4 2 1 5 3 4 6 -5 3 -10 -1 0 3 2 7 2 1 2 3 2
-8 -7 -7 -8
Давайте обозначим символом $$$T$$$ конец раунда. Тогда мы можем нарисовать два графа, соответствующих первому и второму примерам.
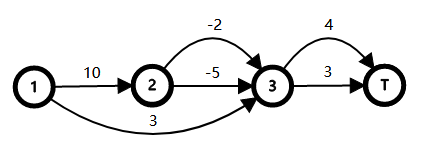
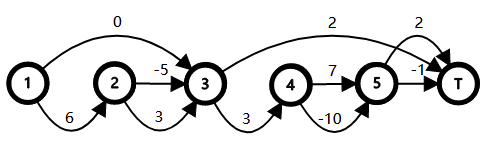
В первом раунде первого примера множество квадратов, через которое вы должны пройти, это $$$\{1\}$$$. Путь, который вы можете использовать, это $$$1\to 3\to T$$$. Его стоимость равна $$$6$$$.
Во втором раунде первого примера множество квадратов, через которое вы должны пройти, это $$$\{1,2\}$$$. Путь, который вы можете использовать, это $$$1\to 2\to 3\to T$$$. Его стоимость равна $$$8$$$.
| Название |
|---|




