| Codeforces Round 715 (Div. 1) |
|---|
| Закончено |
Как преподаватель, Riko Hakozaki часто помогает ученикам в решении задач по различным предметам. Сегодня ее попросили помочь с задачей по программированию, которая заключается в следующем.
Вам выдается неориентированный полный граф с $$$n$$$ вершинами, где для некоторых ребер заданы положительные веса, а для остальных нет. Вам нужно назначить всем еще не назначенным рёбрам неотрицательные веса так, чтобы у получившегося графа XOR (побитовое исключающее ИЛИ) всех весов был равен $$$0$$$.
Определим уродство полного графа как вес его минимального остовного дерева, где вес остовного дерева равен сумме весов его рёбер. Нужно назначить веса так, чтобы уродство получившегося графа было как можно меньше.
Напомним, что неориентированный полный граф с $$$n$$$ вершинами содержит все рёбра $$$(u, v)$$$ с $$$1 \le u < v \le n$$$; такой граф имеет $$$\frac{n(n-1)}{2}$$$ рёбер.
Она не знает, как решить эту задачу, поэтому просит вас решить ее за нее.
Первая строка содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$0 \le m \le \min(2 \cdot 10^5, \frac{n(n-1)}{2} - 1)$$$) — количество вершин и количество предварительно назначенных рёбер. Гарантируется, что есть по крайней мере одно неназначенное ребро.
$$$i$$$-я из следующих строк $$$m$$$ содержит три целых числа $$$u_i$$$, $$$v_i$$$ и $$$w_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u \ne v$$$, $$$1 \le w_i < 2^{30}$$$), обознаающие ребро от $$$u_i$$$ до $$$v_i$$$, которому был назначен вес $$$w_i$$$. Ни одно ребро не появляется во вводе более одного раза.
Выведите в одной строке одно целое число — минимальное уродство среди всех возможных назначений весов с XOR суммой равной $$$0$$$.
4 4 2 1 14 1 4 14 3 2 15 4 3 8
15
6 6 3 6 4 2 4 1 4 5 7 3 4 10 3 5 1 5 2 15
0
5 6 2 3 11 5 3 7 1 4 10 2 4 14 4 3 8 2 5 6
6
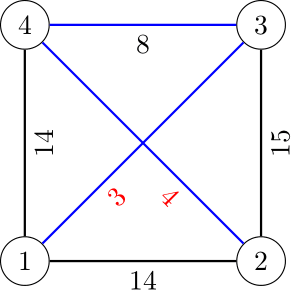
На изображении ниже показан первый пример. Черные веса назначены предварительно, красные веса назначены нами, а минимальное остовное дерево состоит из синих ребер.
| Название |
|---|




