| Codeforces Round 715 (Div. 1) |
|---|
| Закончено |
Любимая последовательность чисел Touko — это перестановка $$$a_1, a_2, \dots, a_n$$$ чисел $$$1, 2, \dots, n$$$, и она хочет коллекцию перестановок, похожих на ее любимую перестановку.
У нее есть коллекция $$$q$$$ отрезков вида $$$[l_i, r_i]$$$ с $$$1 \le l_i \le r_i \le n$$$. Для создания перестановок, похожих на ее любимую перестановку, она придумала следующее определение:
- Перестановка $$$b_1, b_2, \dots, b_n$$$ позволяет интервалу $$$[l', r']$$$ удерживать свою форму, если для любой пары целых $$$(x, y)$$$ таких, что $$$l' \le x < y \le r'$$$, неравенство $$$b_x < b_y$$$ выполняется тогда и только тогда, когда $$$a_x < a_y$$$.
- Перестановка $$$b_1, b_2, \dots, b_n$$$ называется $$$k$$$-похожей, если $$$b$$$ позволяет всем интервалам $$$[l_i, r_i]$$$ для $$$1 \le i \le k$$$ сохранять свою форму.
Yuu хочет найти все $$$k$$$-похожие перестановки для Touko, но это оказалось очень сложной задачей. Вместо этого Yuu будет кодировать набор всех $$$k$$$-похожих перестановок ориентированными ациклическими графами (DAG). Yuu также придумала для себя следующие определения:
- Перестановка $$$b_1, b_2, \dots, b_n$$$ удовлетворяет DAG $$$G'$$$, если для всех ребер $$$u \to v$$$ в $$$G'$$$ выполняется $$$b_u < b_v$$$.
- $$$k$$$-кодирование — это DAG $$$G_k$$$ на наборе вершин $$$1, 2, \dots, n$$$ такой, что перестановка $$$b_1, b_2, \dots, b_n$$$ удовлетворяет $$$G_k$$$, если и только если $$$b$$$ является $$$k$$$-похожей.
Поскольку Yuu сегодня свободна, она хочет выяснить минимальное количество ребер среди всех $$$k$$$-кодирований для каждого $$$k$$$ от $$$1$$$ до $$$q$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$1 \le n \le 25\,000$$$, $$$1 \le q \le 100\,000$$$).
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$, которые образуют перестановку $$$1, 2, \dots, n$$$.
В $$$i$$$-й из следующих строк $$$q$$$ содержатся два целых числа $$$l_i$$$ и $$$r_i$$$. ($$$1 \le l_i \le r_i \le n$$$).
Выведите $$$q$$$ строк. $$$k$$$-я из них должна содержать единственное целое число — минимальное количество рёбер среди всех $$$k$$$-кодирований.
4 3 2 4 1 3 1 3 2 4 1 4
2 4 3
8 4 3 7 4 8 1 5 2 6 3 6 1 6 3 8 1 8
3 5 9 7
10 10 10 5 1 2 7 3 9 4 6 8 2 2 4 5 6 8 4 10 4 4 2 7 2 2 7 8 3 7 2 10
0 1 3 6 6 9 9 9 9 8
Для первого примера:
- Все $$$1$$$-похожие перестановки должны позволять интервалу $$$[1, 3]$$$ удерживать свою форму. Поэтому набор всех $$$1$$$-похожих перестановок составляет $$$\{[3, 4, 2, 1], [3, 4, 1, 2], [2, 4, 1, 3], [2, 3, 1, 4]\}$$$. Оптимальным кодированием этих перестановок является

- Все $$$2$$$-похожие перестановки должны позволять интервалам $$$[1, 3]$$$ и $$$[2, 4]$$$ удерживать свою форму. Поэтому набор всех $$$2$$$-похожих перестановок составляет $$$\{[3, 4, 1, 2], [2, 4, 1, 3]\}$$$. Оптимальным кодированием этих перестановок является

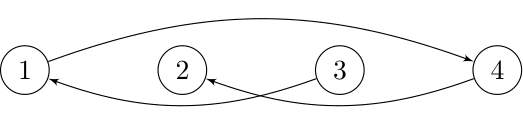
- Все $$$3$$$-похожие перестановки должны позволять интервалы $$$[1, 3]$$$, $$$[2, 4]$$$ и $$$[1, 4]$$$ удерживать свои формы. Поэтому набор всех $$$3$$$-похожих перестановок включает только $$$[2, 4, 1, 3]$$$. Оптимальным кодированием этой перестановки является
| Название |
|---|




