| Codeforces Global Round 14 |
|---|
| Закончено |
В городе Огня, есть $$$n$$$ перекрестков и $$$m$$$ односторонних дорог: $$$i$$$-я дорога ведет от перекрестка $$$a_i$$$ к $$$b_i$$$ и имеет длину $$$l_i$$$ миль.
Также есть $$$q$$$ машин, которые могут передвигаться только по этим дорогам. Машина $$$i$$$ стоит у перекрестка $$$v_i$$$ и оборудована одометром с начальным значением $$$s_i$$$, который увеличивается на один за каждую пройденную милю и сбрасывается в $$$0$$$ когда достигает значения $$$t_i$$$. Фениксу дано задание покататься на машинах по каким-то дорогам (возможно, совсем не двигаться) и вернуться к стартовому перекрестку с одометром, сброшенным в $$$0$$$.
Для каждой машины определите, возможно ли это.
Машина может посещать одни и те же перекрестки и ездить по одним и тем же дорогам произвольное количество раз. Одометры не прекращают считать пройденное расстояние после сброса, а потому одометры можно сбрасывать произвольное количество раз.
В первой строке заданы два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 2 \cdot 10^5$$$; $$$1 \le m \le 2 \cdot 10^5$$$) — количество перекрестков и количество дорог, соответственно.
В каждой из следующих $$$m$$$ строк заданы три целых числа $$$a_i$$$, $$$b_i$$$ и $$$l_i$$$ ($$$1 \le a_i, b_i \le n$$$; $$$a_i \neq b_i$$$; $$$1 \le l_i \le 10^9$$$) — описание $$$i$$$-й дороги. Граф дорог необязательно связный. Гарантируется, что между любой парой перекрестков есть не более одной дороги в каждом направлении.
В следующей строке задано целое число $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — количество машин.
В каждой из следующих $$$q$$$ строк заданы три целых числа $$$v_i$$$, $$$s_i$$$ и $$$t_i$$$ ($$$1 \le v_i \le n$$$; $$$0 \le s_i < t_i \le 10^9$$$) — стартовый перекресток $$$i$$$-й машины, стартовое значение $$$i$$$-го одометра и значение, при котором $$$i$$$-й одометр сбрасывается, соответственно.
Выведите $$$q$$$ ответов. Если одометр $$$i$$$-й машины можно сбросить в $$$0$$$ покатавшись по некоторым дорогам и вернувшись назад в $$$v_i$$$, выведите YES. В противном случае выведите NO.
4 4 1 2 1 2 3 1 3 1 2 1 4 3 3 1 1 3 1 2 4 4 0 1
YES NO YES
4 5 1 2 1 2 3 1 3 1 2 1 4 1 4 3 2 2 1 2 4 4 3 5
YES YES
Ниже представлена иллюстрация первого примера:
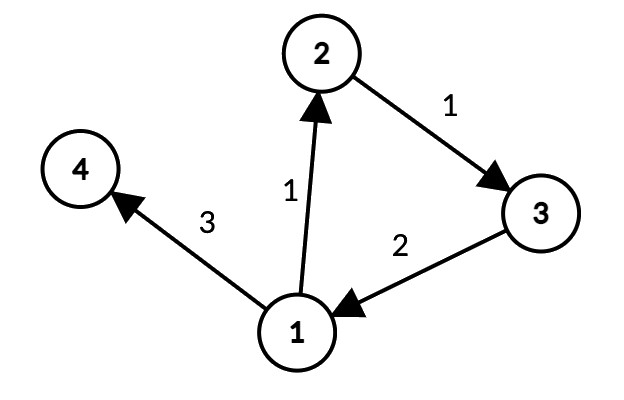
В первом запросе, Феникс может проехать на машине следующем образом: $$$1$$$ $$$\rightarrow$$$ $$$2$$$ $$$\rightarrow$$$ $$$3$$$ $$$\rightarrow$$$ $$$1$$$ $$$\rightarrow$$$ $$$2$$$ $$$\rightarrow$$$ $$$3$$$ $$$\rightarrow$$$ $$$1$$$. Одометр будет сброшен $$$3$$$ раза, и будет показывать $$$0$$$ к концу поездки.
Во втором примере, можно показать, что не существует способа сбросить одометр в $$$0$$$ и при этом вернуться к пересечению $$$1$$$.
В третьем примере, одометр уже показывает $$$0$$$, а поэтому нет необходимости куда-то ехать.
Ниже представлена иллюстрация второго примера:
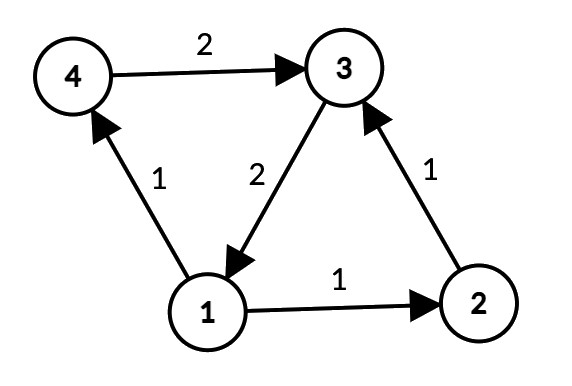
| Название |
|---|




