Маленький Дорми на Рождество получил гистограмму с $$$n$$$ столбцами высоты $$$a_1, a_2, \ldots, a_n$$$. Однако чем больше он играл с гистограммой, тем больше он осознавал ее неидеальность, поэтому сегодня он решил ее немного изменить.
Чтобы изменить гистограмму, маленький Дорми может выполнить следующую операцию произвольное количество раз:
- Выбрать индекс $$$i$$$ ($$$1 \le i \le n$$$) такой, что $$$a_i>0$$$, и присвоить $$$a_i := a_i-1$$$.
Маленький Дорми определяет уродливость гистограммы (после выполнения некоторого количества операций) как сумму длин вертикальных отрезков границы гистограммы и количества операций, которые он сделал. Чтобы получить лучшую гистограмму, он хочет минимизировать ее уродливость, применив несколько операций.
Так как гистограмма очень большая, маленькому Дорми сложно вычислить минимально возможную уродливость, поэтому, как старший брат Дорми, вы должны помочь ему найти минимально возможную уродливость.
Рассмотрим пример, в котором изначально в гистограмме $$$4$$$ столбца, высоты которых равны $$$4,8,9,6$$$:
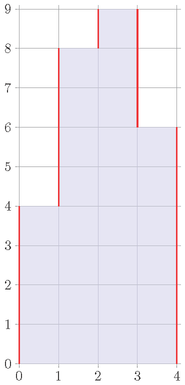
Синим показана гистограмма, а красные линии показывают вертикальные отрезки границы гистограммы. В настоящий момент сумма длин вертикальных отрезков границы равна $$$4+4+1+3+6 = 18$$$, поэтому, если Дорми не будет изменять гистограмму, ее уродливость будет равна $$$18$$$.
Если Дорми применит операцию один раз к столбцу $$$2$$$ и два раза к столбцу $$$3$$$, столбцы будут иметь высоты $$$4,7,7,6$$$:
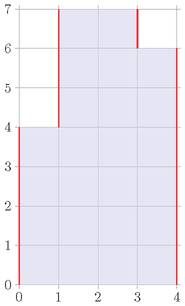
Теперь общая длина вертикальных отрезков границы равна $$$4+3+1+6=14$$$, а уродливость равна $$$14+3=17$$$. Можно показать, что это — оптимальное решение.
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
Первая строка набора входных данных содержит целое число $$$n$$$ ($$$1 \le n \le 4 \cdot 10^5$$$).
Вторая строка набора входных данных содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$0 \le a_i \le 10^9$$$).
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$4 \cdot 10^5$$$.
Для каждого набора выходных данных выведите одно целое число: минимально возможную уродливость, которую может получить Дорми.
2 4 4 8 9 6 6 2 1 7 4 0 0
17 12
Пример $$$1$$$ описан в условии задачи.
Изначальная гистограмма в примере $$$2$$$ показана ниже:
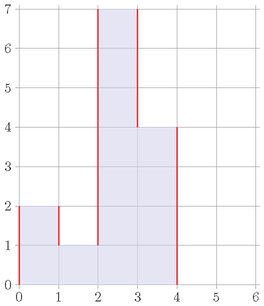
Изначально уродливость равна $$$2+1+6+3+4=16$$$.
Применяя операцию один раз к столбцу $$$1$$$, шесть раз к столбцу $$$3$$$ и три раза к столбцу $$$4$$$, получится гистограмма с высотами $$$1,1,1,1,0,0$$$:
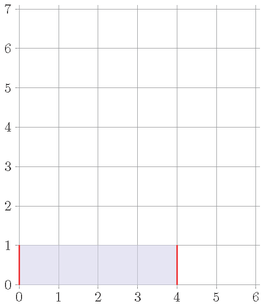
Длина вертикальных отрезков границы теперь равна $$$1+1=2$$$, а маленький Дорми сделал $$$1+6+3=10$$$ операций, поэтому общая уродливость равна $$$2+10=12$$$, что является оптимальным решением.
| Название |
|---|




