Это интерактивная задача.
Так как маленький Эрики прошел на Международную олимпиаду школьников по информатике в этом году, он получил подарок от своих друзей: дерево с $$$n$$$ вершинами!
По пути к месту проведения Эрики было скучно, поэтому он решил сыграть в игру с маленьким Ивонном с использованием нового дерева. Сначала Ивонн загадывает две (не обязательно различные) вершины $$$a$$$ и $$$b$$$ в этом дереве (не сообщая их Эрики), а затем сообщает ему подсказку $$$f$$$ — одну из вершин на простом пути от $$$a$$$ до $$$b$$$.
Затем маленький Эрики может спрашивать следующие вопросы:
- Если подвесить дерево за вершину $$$r$$$ (Эрики может выбрать $$$r$$$), какая вершина будет наименьшим общим предком вершин $$$a$$$ и $$$b$$$?
Задача маленького Эрики — найти вершины $$$a$$$ и $$$b$$$.
Маленький Ивонн считает игру слишком простой, поэтому в начале игры, перед тем, как дать подсказку $$$f$$$, он просит Эрики найти максимальное количество запросов, необходимых для нахождения $$$a$$$ и $$$b$$$ для всех возможных значений $$$a$$$, $$$b$$$ и $$$f$$$ в предположении, что Эрики действует оптимально. Под оптимальными действиями подразумевается стратегия, делающая наименьшее число запросов. Конечно, после того, как маленький Эрики скажет это максимальное количество запросов, Ивонн не разрешит сделать больше запросов в самой игре.
Дерево, $$$a$$$, $$$b$$$ и $$$f$$$ фиксированы до начала игры и не меняются в зависимости от запросов.
Сначала считайте строку, содержащую одно целое число $$$n$$$ ($$$1 \le n \le 10^5$$$) — количество вершин в дереве.
Сделающие $$$n−1$$$ строк описывают дерево маленького Дорми. Каждая из этих строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), обозначающие ребро между вершинами $$$u$$$ и $$$v$$$ ($$$u \neq v$$$). Гарантируется, что эти ребра образуют дерево.
После этого вы должны вывести $$$k$$$ — максимальное число запросов, необходимое для определения $$$a$$$ и $$$b$$$ по всем возможным значениям $$$a$$$, $$$b$$$ и $$$f$$$ в предположении оптимальной игры. Вы должны вывести перевод строки и сбросить буфер вывода после вывода $$$k$$$.
Затем считайте одно целое число $$$f$$$ ($$$1 \le f \le n$$$) — подсказку: вершину на пути от $$$a$$$ до $$$b$$$ включительно.
После этого вы можете делать запросы. Вам будет разрешено сделать не более $$$k$$$ запросов, где $$$k$$$ — число, которое вы вывели.
Для того, чтобы сделать запрос, выведите «? r», где $$$r$$$ — целое число, $$$1 \le r \le n$$$, обозначающее, за какую вершину вы хотите подвесить дерево.
В ответ вы получите целое число $$$x$$$ ($$$1 \le x \le n$$$) — наименьший общий предок вершин $$$a$$$ и $$$b$$$, если дерево подвесить за $$$r$$$.
Когда ваша программа определит $$$a$$$ и $$$b$$$, выведите их в следующем формате: «! a b», где $$$a$$$ и $$$b$$$ — две загаданные вершины, и завершите программу сразу после сброса буфера вывода. Вы можете вывести $$$a$$$ и $$$b$$$ в любом порядке.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Если вы сделаете некорректный вывод, или сделаете более $$$k$$$ запросов, взаимодействие прекратится и вы получите вердикт «Неправильный ответ». Вывод считается некорректным, если это некорректный запрос, или вы вывели $$$k$$$, меньшее $$$0$$$ или большее $$$n$$$.
Взломы
Чтобы взломать решение, используйте следующий формат:
Первая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 10^5$$$).
Следующие $$$n−1$$$ строк содержат по два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), обозначающие ребро между вершинами $$$u$$$ и $$$v$$$ ($$$u \neq v$$$). Эти $$$n-1$$$ ребра должны образовывать дерево.
Следующая строка содержит два целых числа $$$a$$$ и $$$b$$$ ($$$1 \le a,b \le n$$$).
Последняя строка должна содержать одно целое число $$$f$$$ ($$$1 \le f \le n$$$). Вершина $$$f$$$ должна лежать на простом пути от $$$a$$$ до $$$b$$$ включительно.
4 3 2 2 1 2 4 1 1 2 2
3 ? 1 ? 2 ? 3 ! 4 1
5 3 1 1 4 4 5 4 2 1 4 1 4
3 ? 4 ? 1 ? 5 ! 1 4
Дерево из первого примера показано ниже. Вершины $$$a$$$ и $$$b$$$ выделены жирным.
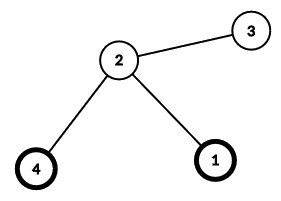
Обратите внимание, что вы можете вывести $$$a$$$ и $$$b$$$ в любом порядке.
Ниже приведены ответы на все возможные запросы $$$1,2,\ldots,n$$$:
- $$$1$$$: $$$1$$$
- $$$2$$$: $$$2$$$
- $$$3$$$: $$$2$$$
- $$$4$$$: $$$4$$$
__________________________________________
Дерево из второго примера показано ниже. Вершины $$$a$$$ и $$$b$$$ выделены жирным.
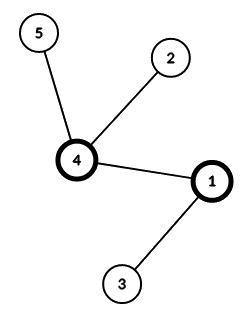
Ниже приведены ответы на все возможные запросы $$$1,2,\ldots,n$$$ в примере $$$2$$$:
- $$$1$$$: $$$1$$$
- $$$2$$$: $$$4$$$
- $$$3$$$: $$$1$$$
- $$$4$$$: $$$4$$$
- $$$5$$$: $$$4$$$
| Название |
|---|




