| Codeforces Round 726 (Div. 2) |
|---|
| Закончено |
У вас есть связный неориентированный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер. У $$$i$$$-го узла есть начальное значение $$$v_i$$$ и целевое значение $$$t_i$$$.
За одну операцию можно выбрать любое ребро $$$(i, j)$$$ и добавить $$$k$$$ к $$$v_i$$$ и $$$v_j$$$, где $$$k$$$ может быть любым целым числом. В частности, $$$k$$$ может быть отрицательным.
Ваша задача определить, можно ли, выполнив некоторое конечное число операций (возможно, ноль), добиться того, что каждого узла $$$i$$$, $$$v_i = t_i$$$.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$), количество наборов входных данных. Затем следуют наборы входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$, $$$m$$$ ($$$2 \leq n \leq 2\cdot 10^5$$$, $$$n-1\leq m\leq \min(2\cdot 10^5, \frac{n(n-1)}{2})$$$) — количество вершин и ребер соответственно.
Вторая строка содержит $$$n$$$ целых чисел $$$v_1\ldots, v_n$$$ ($$$-10^9 \leq v_i \leq 10^9$$$) — начальные значения вершин.
Третья строка содержит $$$n$$$ целых чисел $$$t_1\ldots, t_n$$$ ($$$-10^9 \leq t_i \leq 10^9$$$) — целевые значения вершин.
Каждая из следующих $$$m$$$ строк содержит два целых числа $$$i$$$ и $$$j$$$, обозначающих ребро между вершинами $$$i$$$ и $$$j$$$ ($$$1 \leq i, j \leq n$$$, $$$i\ne j$$$).
Гарантируется, что граф связный и между одной парой вершин есть не более одного ребра.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$, а сумма $$$m$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$.
Для каждого наборам входных данных, если возможно, чтобы значение в каждой вершине стало равно целевому после некоторого количества операций, выведите «YES». В противном случае выведите «NO».
2 4 4 5 1 2 -3 3 3 10 1 1 2 1 4 3 2 3 4 4 4 5 8 6 6 -3 1 15 4 1 2 1 4 3 2 3 4
YES NO
Вот визуализация первого тестового случая (оранжевые значения обозначают начальные значения, а синие — целевые):
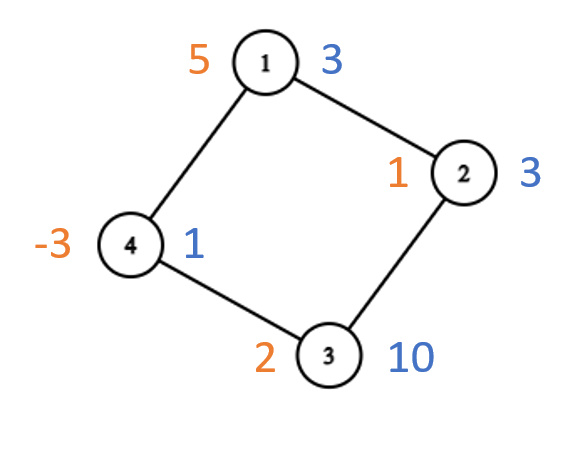
Один из возможных порядков действий для получения нужных значений для каждого узла следующий:
- Операция $$$1$$$: Добавить $$$2$$$ к вершинами $$$2$$$ и $$$3$$$.
- Операция $$$2$$$: Добавить $$$-2$$$ к вершинам $$$1$$$ и $$$4$$$.
- Операция $$$3$$$: Добавить $$$6$$$ к вершинам $$$3$$$ и $$$4$$$.
Теперь мы видим, что в общей сложности мы добавили $$$-2$$$ к вершине $$$1$$$, $$$2$$$ к вершине $$$2$$$, $$$8$$$ к вершине $$$3$$$ и $$$4$$$ к вершине $$$4$$$, что привело каждую вершину к нужному значению.
Для графа из второго набора входных данных получить нужные значения невозможно.
| Название |
|---|




