| Codeforces Round 731 (Div. 3) |
|---|
| Закончено |
На бесконечном клетчатом поле отмечены три различные клетки: $$$A$$$, $$$B$$$ и $$$F$$$. Выведите длину кратчайшего пути из $$$A$$$ в $$$B$$$, если:
- за один ход можно переходить на любую из четырех соседних по стороне клеток;
- посещать клетку $$$F$$$ — запрещено (она является препятствием).
В первой строке записано одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных в тесте. Далее следуют описания $$$t$$$ наборов входных данных, перед каждым из них входные данные содержат пустую строку.
Каждый набор входных данных состоит из трех строк. Первая из них содержит два целых числа $$$x_A, y_A$$$ ($$$1 \le x_A, y_A \le 1000$$$) — координаты стартовой клетки $$$A$$$. Вторая из них содержит два целых числа $$$x_B, y_B$$$ ($$$1 \le x_B, y_B \le 1000$$$) — координаты конечной клетки $$$B$$$. Третья строка содержит два целых числа $$$x_F, y_F$$$ ($$$1 \le x_F, y_F \le 1000$$$) — координаты клетки $$$F$$$, которая является препятствием. Все три клетки — различны.
Координата $$$x$$$ соответствует номеру столбца, а $$$y$$$ — номеру строки (см. картинки ниже).
Выведите $$$t$$$ строк. $$$i$$$-я из них должна содержать ответ для $$$i$$$-го набора входных данных — длину кратчайшего пути из клетки $$$A$$$ в клетку $$$B$$$, если клетка $$$F$$$ запрещена для посещения.
7 1 1 3 3 2 2 2 5 2 1 2 3 1000 42 1000 1 1000 1000 1 10 3 10 2 10 3 8 7 8 3 7 2 1 4 1 1 1 1 344 1 10 1 1
4 6 41 4 4 2 334
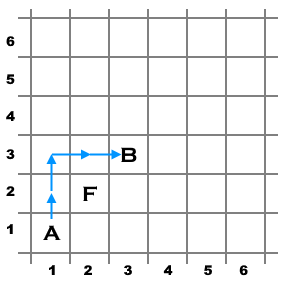 Пример возможного кратчайшего пути для первого набора входных данных.
Пример возможного кратчайшего пути для первого набора входных данных. 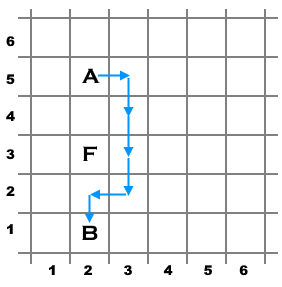 Пример возможного кратчайшего пути для второго набора входных данных.
Пример возможного кратчайшего пути для второго набора входных данных.
| Название |
|---|




