| Codeforces Round 731 (Div. 3) |
|---|
| Закончено |
Задан ориентированный граф $$$G$$$, в котором допустимы петли (то есть рёбра из вершины в себя). В $$$G$$$ отсутствуют кратные рёбра, то есть для каждой упорядоченной пары вершин $$$(u, v)$$$ существует не более одного ребра из $$$u$$$ в $$$v$$$. Вершины пронумерованы от $$$1$$$ до $$$n$$$.
Назовём путем из $$$u$$$ в $$$v$$$ такую последовательность рёбер, что:
- вершина $$$u$$$ является началом первого ребра пути;
- вершина $$$v$$$ является концом последнего ребра пути;
- для любой пары соседних рёбер следующее ребро начинается с вершины, на которую заканчивается предыдущее ребро.
Дополнительно будем считать, что пустая последовательность рёбер — это путь из $$$u$$$ в $$$u$$$.
Для каждой вершины $$$v$$$ выведите одно из четырёх значений:
- $$$0$$$, если не существует пути из $$$1$$$ в $$$v$$$;
- $$$1$$$, если существует ровно один путь из $$$1$$$ в $$$v$$$;
- $$$2$$$, если существует более одного пути из $$$1$$$ в $$$v$$$ и это число является конечной величиной;
- $$$-1$$$, если существует бесконечно много путей из $$$1$$$ в $$$v$$$.
Рассмотрим пример, изображённый на рисунке.
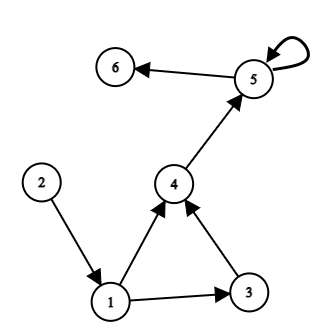
Тогда:
- ответ для вершины $$$1$$$ равен $$$1$$$: существует ровно один путь из $$$1$$$ в $$$1$$$ (путь длины $$$0$$$);
- ответ для вершины $$$2$$$ равен $$$0$$$: не существует пути из $$$1$$$ в $$$2$$$;
- ответ для вершины $$$3$$$ равен $$$1$$$: существует ровно один путь из $$$1$$$ в $$$3$$$ (это ребро $$$(1, 3)$$$);
- ответ для вершины $$$4$$$ равен $$$2$$$: существует более одного, но конечное число путей из $$$1$$$ в $$$4$$$ (два пути: $$$[(1, 3), (3, 4)]$$$ и $$$[(1, 4)]$$$);
- ответ для вершины $$$5$$$ равен $$$-1$$$: существует бесконечно много путей из $$$1$$$ в $$$5$$$ (петля может быть использована в пути сколько угодно раз);
- ответ для вершины $$$6$$$ равен $$$-1$$$: существует бесконечно много путей из $$$1$$$ в $$$6$$$ (петля может быть использована в пути сколько угодно раз).
В первой строке записано целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных в тесте. Далее заданы описания $$$t$$$ наборов входных данных. Перед каждым из них в тесте содержится пустая строка.
В первой строке набора входных данных записаны два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 4 \cdot 10^5, 0 \le m \le 4 \cdot 10^5$$$) — количество вершин и рёбер в графе, соответственно. Далее входные данные содержат $$$m$$$ строк с описаниями рёбер. Каждая строка состоит из двух целых чисел $$$a_i$$$, $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$) — начало и конец $$$i$$$-го ребра. Вершины графа пронумерованы от $$$1$$$ до $$$n$$$. Заданный граф может содержать петли (допустимо $$$a_i = b_i$$$), но не может содержать кратных рёбер (недопустимо $$$a_i = a_j$$$ и $$$b_i = b_j$$$ для $$$i \ne j$$$).
Сумма значений $$$n$$$ по всем наборам входных данных в тесте не превосходит $$$4 \cdot 10^5$$$. Аналогично, сумма значений $$$m$$$ по всем наборам входных данных в тесте не превосходит $$$4 \cdot 10^5$$$.
Выведите $$$t$$$ строк. $$$i$$$-я строка должна содержать ответ на $$$i$$$-й набор входных данных — последовательность $$$n$$$ целых чисел от $$$-1$$$ до $$$2$$$.
5 6 7 1 4 1 3 3 4 4 5 2 1 5 5 5 6 1 0 3 3 1 2 2 3 3 1 5 0 4 4 1 2 2 3 1 4 4 3
1 0 1 2 -1 -1 1 -1 -1 -1 1 0 0 0 0 1 1 2 1
| Название |
|---|




