| Codeforces Round 736 (Div. 1) |
|---|
| Закончено |
Это сложная версия задачи. Единственное отличие от простой версии заключается в том, что в данной версии координаты могут быть как чётными, так и нечётными.
Даны $$$n$$$ столбов, расположенных в различных точках на плоскости. Гарантируется, что никакие три столба не лежат на одной прямой.
На плоскости также есть бесконечное количество коров, по одной в каждой точке с целочисленными координатами.
Грегор — член общества иллюминатов и хочет построить треугольный загон, соединив $$$3$$$ различных существующих столба забором. Корова, находящаяся строго внутри загона, считается огражденной. Если ограждено нечётное число коров, и при этом площадь загона равна целому числу, то загон считается интересным.
Найдите количество интересных загонов.
Первая строка содержит одно целое число $$$n$$$ ($$$3 \le n \le 6000$$$) — количество столбов, которые Грегор может выбрать в качестве вершин загона.
Следующие $$$n$$$ строк содержат по два целых числа $$$x$$$ и $$$y$$$ ($$$0 \le x,y \le 10^7$$$, где $$$(x,y)$$$ — координата очередного столба. Все столбы расположены в различных точках. Никакие три столба не лежат на одной прямой.
Напечатайте одно целое число — количество интересных загонов. Два загона считаются различными, если они образованы различными множествами трех столбов.
3 0 0 2 0 0 4
1
4 1 8 0 6 5 2 5 6
1
10 170 59 129 54 5 98 129 37 58 193 154 58 24 3 13 138 136 144 174 150
29
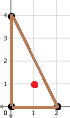
В первом примере существует только $$$1$$$ загон. Этот загон является интересным, поскольку его площадь равна $$$4$$$ и есть $$$1$$$ пойманная корова, помеченная красным.
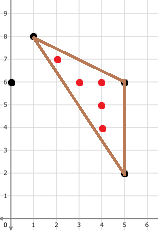
Во втором примере существует $$$4$$$ возможных загона. Однако, только один из них является интересным. Этот загон имеет площадь, равную $$$8$$$, и $$$5$$$ пойманных коров.
| Название |
|---|




