| Codeforces Global Round 15 |
|---|
| Закончено |
Числа $$$1, \, 2, \, \dots, \, n \cdot k$$$ окрашены в $$$n$$$ цветов. Эти цвета обозначены $$$1, \, 2, \, \dots, \, n$$$. Для каждого $$$1 \le i \le n$$$ существует ровно $$$k$$$ чисел, окрашенных в цвет $$$i$$$.
Пусть $$$[a, \, b]$$$ обозначает отрезок целых чисел от $$$a$$$ до $$$b$$$ включительно, то есть множество $$$\{a, \, a + 1, \, \dots, \, b\}$$$. Вы должны выбрать $$$n$$$ отрезков $$$[a_1, \, b_1], \, [a_2, \, b_2], \, \dots, [a_n, \, b_n]$$$ таких, что:
- для каждого $$$1 \le i \le n$$$ имеет место $$$1 \le a_i < b_i \le n \cdot k$$$;
- для каждого $$$1 \le i \le n$$$, числа $$$a_i$$$ и $$$b_i$$$ окрашены цветом $$$i$$$;
- каждое число $$$1 \le x \le n \cdot k$$$ принадлежит не более чем $$$\left\lceil \frac{n}{k - 1} \right\rceil$$$ отрезкам.
Можно показать, что такое семейство отрезков всегда существует при заданных ограничениях.
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n \le 100$$$, $$$2 \le k \le 100$$$) — количество цветов и количество вхождений каждого цвета.
Вторая строка содержит $$$n \cdot k$$$ целых чисел $$$c_1, \, c_2, \, \dots, \, c_{nk}$$$ ($$$1 \le c_j \le n$$$), где $$$c_j$$$ — цвет числа $$$j$$$. Гарантируется, что для каждого $$$1 \le i \le n$$$ $$$c_j = i$$$ имеет место для ровно $$$k$$$ различных индексов $$$j$$$.
Выведите $$$n$$$ строк. В $$$i$$$-й строке должны содержаться два целых числа $$$a_i$$$ и $$$b_i$$$.
Если существует несколько допустимых вариантов выбрать отрезки, выведите любой.
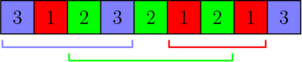
4 3 2 4 3 1 1 4 2 3 2 1 3 4
4 5 1 7 8 11 6 12
1 2 1 1
1 2
3 3 3 1 2 3 2 1 2 1 3
6 8 3 7 1 4
2 3 2 1 1 1 2 2
2 3 5 6
В первой выборке каждое число может содержаться не более чем в $$$\left\lceil \frac{4}{3 - 1} \right\rceil = 2$$$ отрезках. Вывод описывается следующим рисунком:

Во втором примере единственным отрезком, который можно выбрать, является $$$[1, \, 2]$$$, и каждое число действительно содержится не более чем в $$$\left\lceil \frac{1}{2 - 1} \right\rceil = 1$$$ отрезках.
В третьем примере, каждое число может содержаться не более чем в $$$\left\lceil \frac{3}{3 - 1} \right\rceil = 2$$$ отрезках. Вывод описывается следующим рисунком:
| Название |
|---|




