| Codeforces Global Round 15 |
|---|
| Закончено |
Назовем точку плоскости допустимой, если ее координаты — положительные целые числа, не превышающие $$$200$$$.
Есть невидимый прямоугольник такой, что:
- его вершины все допустимы;
- его стороны параллельны координатным осям;
- его площадь строго положительна.
Для того чтобы его угадать, вы можете задать не более $$$4$$$ запросов.
В каждом запросе вы выбираете непустое подмножество допустимых точек, и вам говорят, сколько из выбранных точек находится внутри или на границе невидимого прямоугольника.
Чтобы задать запрос (такой, который описан в утверждении), нужно вывести две строки:
- В первой строке выведите «? $$$k$$$» (без кавычек), где $$$k$$$ ($$$k\ge 1$$$) — количество выбранных точек.
- Во второй строке выведите $$$2k$$$ целых чисел $$$x_1,\, y_1,\, x_2,\, y_2,\, \dots,\, x_k,\, y_k$$$ ($$$1\le x_i,y_i\le 200$$$ для $$$i=1,2,\dots,k$$$), где $$$(x_1, y_1),\,(x_2, y_2),\,(x_3, y_3),\, \dots,\,(x_k, y_k)$$$ — это $$$k$$$ попарно различных допустимых выбранных точек (порядок точек не важен).
Когда вы определите периметр $$$p$$$ невидимого прямоугольника, вы должны вывести «! $$$p$$$» (без кавычек) и завершить свою программу.
Если вы зададите более $$$4$$$ запросов или один из запросов будет некорректным, интерактор немедленно завершит работу, а ваша программа получит вердикт Неправильный ответ.
Интерактор может быть адаптивным (т.е. скрытый прямоугольник может быть не выбран до начала взаимодействия).
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Hacks
Чтобы взломать решение, используйте следующий формат.
Выведите только одну строку, содержащую $$$4$$$ целых числа $$$x_0$$$, $$$y_0$$$, $$$x_1$$$, $$$y_1$$$ ($$$1\le x_0<x_1\le 200$$$, $$$1\le y_0 < y_1 \le 200$$$), где $$$(x_0,y_0)$$$ — левая нижняя вершина скрытого прямоугольника, $$$(x_1, y_1)$$$ - правая верхняя вершина скрытого прямоугольника.
Обратите внимание, что для взломов взаимодействие не будет адаптивным.
13 5 123 80
2 2 4 4
1 1 200 200
Ниже приведен пример взаимодействия для первого примера, призванный показать формат запросов. $$$$$$ \begin{array}{l|l|l} \text{Запрос (программа участника)} & \text{Ответ (интерактор)} & \text{Пояснение}\\ \hline \mathtt{?\ 4} & & \text{Мы выбрали $4$ вершины} \\ \mathtt{13\ 5\ 13\ 80\ 123\ 5\ 123\ 80} & \mathtt{4} &\text{скрытого прямоугольника.}\\ \hline \mathtt{?\ 5} & & \text{Мы выбрали $4$ точки за пределами скрытого}\\ \mathtt{100\ 4\ 100\ 81\ 12\ 40\ 124\ 40\ 50\ 50} & \mathtt{1} & \text{прямоугольника, а также точку $(50,50)$.}\\ \hline \mathtt{?\ 2} & & \text{Выбираем точки $(1, 1)$} \\ \mathtt{200\ 200\ 1\ 1} & \mathtt{0} & \text{и $(200,200)$.}\\ \hline \mathtt{!\ 370} & & \text{Это правильный периметр.} \end{array} $$$$$$
Для второго образца, возможное взаимодействие следующее. $$$$$$ \begin{array}{l|l|l|l} \text{Запрос (программа участника)} & \text{Ответ (интерактор)} & \text{Пояснение} \\ \hline \mathtt{?\ 4} & & \text{Мы выбираем точки $(3, 2)$, $(4, 1)$,} \\ \mathtt{3\ 2\ 4\ 1\ 5\ 2\ 4\ 3} & 2 & \text{$(5, 2)$ и $(4, 3)$.} \\ \hline \mathtt{?\ 7} & & \text{Мы выбираем точки $(1, 4)$, $(2, 4)$,} \\\\\ \mathtt{1\ 4\ 2\ 4\ 1\ 5\ 2\ 5\ 5\ 5\ 5\ 5\ 6\ 6\ 5} & 1 & \text{$(1, 5)$, $(2, 5)$, $(5, 5)$, $(5, 6)$ и $(6, 5)$.} \\ \hline \mathtt{!\ 8} & & \text{Это правильный периметр.} \end{array} $$$$$$ Ситуация показана на следующем рисунке:
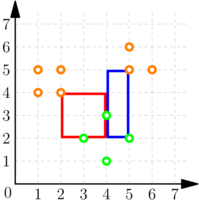
Зеленые точки — это точки, относящиеся к первому запросу, а оранжевые — ко второму. Видно, что существует ровно два прямоугольника, соответствующих ответам собеседника:
- прямоугольник вершин $$$(2, 2)$$$ и $$$(4, 4)$$$, показанный красным цветом;
- прямоугольник из вершин $$$(4, 2)$$$ и $$$(5, 5)$$$, показанный синим цветом.
| Название |
|---|




