
Как уже упоминалось, Василий любит играть в компьютерные игры. В одной из его любимых игр персонаж находится во вселенной, где каждая планета обозначается двоичным числом от $$$0$$$ до $$$2^n - 1$$$. На каждой из планет находятся врата, позволяющие перемещаться с планеты $$$i$$$ на планету $$$j$$$, если двоичная запись $$$i$$$ отличается от двоичной записи $$$j$$$ ровно в одном бите.
Василий хочет проверить вас и посмотреть, как вы справитесь с обработкой следующих запросов в этом игровом мире:
- Уничтожить планеты с номерами от $$$l$$$ до $$$r$$$ включительно. На такие планеты больше нельзя перемещаться.
- Узнать, можно ли с планеты $$$a$$$ долететь до планеты $$$b$$$, используя какое-то количество планетных врат. Гарантируется, что планеты $$$a$$$ и $$$b$$$ не являются уничтоженными.
Первая строка содержит два целых числа $$$n$$$, $$$m$$$ ($$$1 \leq n \leq 50$$$, $$$1 \leq m \leq 5 \cdot 10^4$$$) — количество бит в двоичной записи каждой планеты и количество запросов соответственно.
Следующие $$$m$$$ строк ввода содержат запросы двух видов:
block l r — запрос на уничтожение планет, с номерами от $$$l$$$ до $$$r$$$ включительно ($$$0 \le l \le r < 2^n$$$). Гарантируется, что никакая планета не будет уничтожена дважды.
ask a b — запрос на достижимость между планетами $$$a$$$ и $$$b$$$ ($$$0 \le a, b < 2^n$$$). Гарантируется, что планеты $$$a$$$ и $$$b$$$ еще не были уничтожены.
На каждый запрос типа ask в отдельной строке необходимо вывести «1», если с планеты $$$a$$$ можно долететь до планеты $$$b$$$, и «0» иначе (без кавычек).
3 3 ask 0 7 block 3 6 ask 0 7
1 0
6 10 block 12 26 ask 44 63 block 32 46 ask 1 54 block 27 30 ask 10 31 ask 11 31 ask 49 31 block 31 31 ask 2 51
1 1 0 0 1 0
Первый тест можно визуализировать следующим образом:
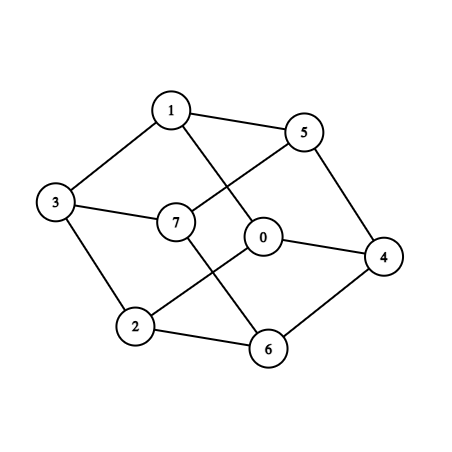
Ответ на запрос ask 0 7 положительный.
Далее после запроса block 3 6 граф будет выглядеть следующим образом (выделены уничтоженные вершины):
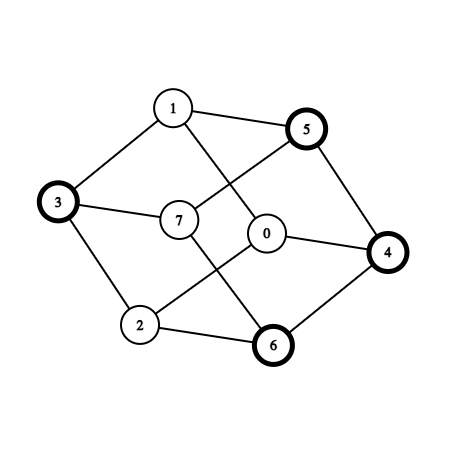
Ответ на запрос ask 0 7 отрицательный, так как любой путь из вершины $$$0$$$ в вершину $$$7$$$ лежит через одну из уничтоженных вершин.
| Название |
|---|




