| Codeforces Round 738 (Div. 2) |
|---|
| Закончено |
Это простая версия задачи. Две версии отличаются ограничениями на $$$n$$$. Вы можете делать взломы, только если обе версии задачи решены.
Лесом называется неориентированный граф без циклов (не обязательно связный).
Mocha и Diana — друзья из Чжицзяна, у каждой из них есть лес с вершинами, пронумерованными от $$$1$$$ до $$$n$$$, и они хотят добавить ребра в свои леса с выполнением следующих условий:
- После добавления ребер каждый из графов остается лесом.
- Они добавляют одинаковые ребра. Это значит, что если ребро $$$(u, v)$$$ добавляется в лес Mocha, то также ребро $$$(u, v)$$$ добавляется в лес Diana, и наоборот.
Mocha и Diana хотят знать, какое максимальное количество ребер они могут добавить, и какие ребра им нужно добавлять.
Первая строка содержит три целых числа $$$n$$$, $$$m_1$$$ и $$$m_2$$$ ($$$1 \le n \le 1000$$$, $$$0 \le m_1, m_2 < n$$$) — количество вершин и начальное количество ребер в лесе Mocha и в лесе Diana, соответственно.
Каждая из следующих $$$m_1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$) — ребра в лесе Mocha.
Каждая из следующих $$$m_2$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$) — ребра в лесе Diana.
Первая строка содержит одно целое число $$$h$$$ — максимальное количество ребер, которое можно добавить в каждый из лесов Mocha и Diana.
Каждая из следующих $$$h$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$) — ребра, которые нужно добавить.
Если существует несколько решений, выведите любое из них.
3 2 2 1 2 2 3 1 2 1 3
0
5 3 2 5 4 2 1 4 3 4 3 1 4
1 2 4
8 1 2 1 7 2 6 1 5
5 5 2 2 3 3 4 4 7 6 8
В первом примере нельзя добавить ни одно ребро.
Во втором примере начальные леса выглядят следующим образом.
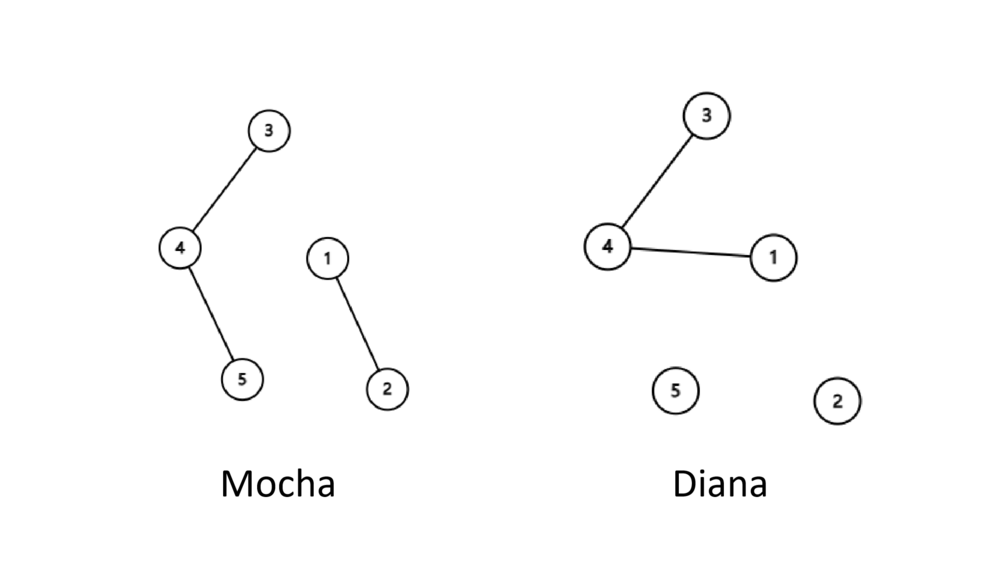
Можно добавить ребро $$$(2, 4)$$$.
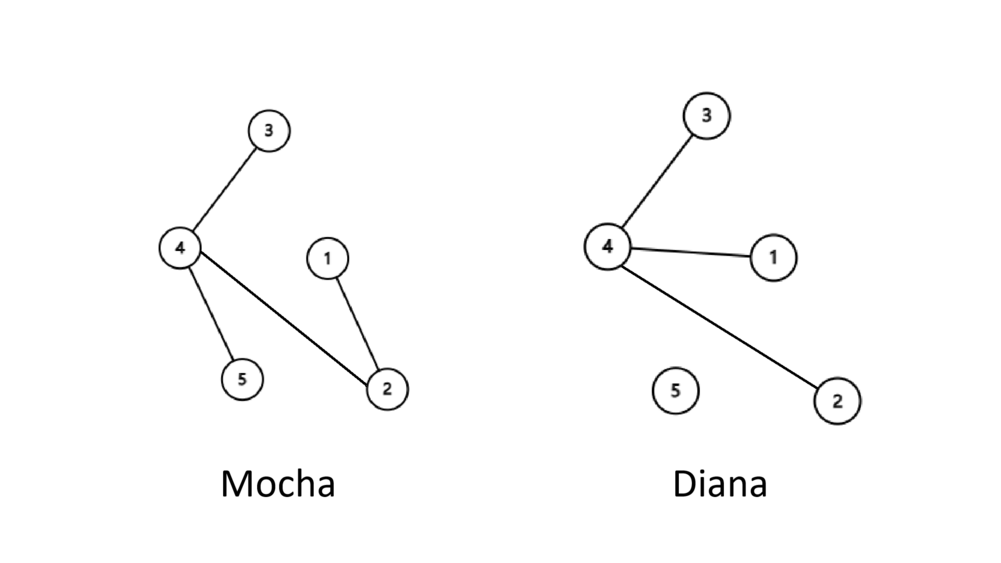
| Название |
|---|




