| Codeforces Round 110 (Div. 1) |
|---|
| Закончено |
Миссис Хадсон давно не пекла свои знаменитые оладьи, и вот, наконец, решила испечь их вновь. Недавно она узнала m новых рецептов, и ей не терпится их опробовать. Эти рецепты основываются на n особых приправах. На кухне у миссис Хадсон все эти приправы лежат в баночках, пронумерованных целыми числами от 0 до n - 1 (каждая приправа лежит в своей баночке). На каждой баночке также написана цена соответствующей приправы — некоторое целое число ai.
Для i-ого рецепта оладий известно три величины: di, si, ci. Здесь di и ci — целые числа, а si — шаблон некоторого целого числа, записанного в системе счисления с основанием di. Шаблон содержит цифры, латинские буквы (для обозначения цифр больше девяти) и знаки вопроса. Число x в di-ичной системе счисления подходит под шаблон si, если в шаблоне можно заменить знаки вопроса на цифры и буквы так, чтобы получилось число x (лидирующие нули не учитываются при сравнении). Более формально: каждый знак вопроса нужно заменить ровно одной цифрой или буквой. Если после замены всех вопросов получилось число с лидирующими нулями, эти нули можно отбросить. Например, число 40A9875 в 11-ичной системе счисления подходит под шаблон «??4??987?», а число 4A9875 — не подходит.
Чтобы приготовить оладьи по i-ому рецепту, необходимо взять все баночки, номера которых, переведенные в di-ичную систему счисления, подходят под шаблон si. Контрольным числом рецепта (zi) называется сумма числа ci и произведения цен всех взятых баночек. Более формально: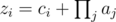 
(где j — все такие числа, которые в системе счисления с основанием di подходят под шаблон si). Если ни одна из баночек не подходит под шаблон, то произведение равно 1, а контрольное число равно ci + 1.
Миссис Хадсон не так интересны сами контрольные числа, как их минимальные простые делители. Ваша задача — найти для каждого рецепта i минимальный простой делитель числа zi. Если этот делитель больше 100, то его искать не требуется — выведите -1.
В первой строке записано единственное целое число n (1 ≤ n ≤ 104). Во второй строке через пробел перечислены цены приправ a0, a1, ..., an - 1, где ai — целое число (1 ≤ ai ≤ 1018).
В третьей строке записано единственное целое число m (1 ≤ m ≤ 3·104) — количество рецептов, которые узнала миссис Хадсон.
В следующих m строках описаны рецепты, по одному на каждой строке. Сначала задано целое число di, записанное в десятичной системе исчисления (2 ≤ di ≤ 16). Далее, через пробел, записан шаблон si — строка длиной от 1 до 30 включительно, состоящая из цифр от «0» до «9», букв от «A» до «F» и знаков «?». Буквы от «A» до «F» следует считать цифрами от 10 до 15 соответственно. Гарантируется, что все цифры шаблона (в том числе, обозначаемые буквами) строго меньше, чем di. Далее, через пробел, задано целое число ci, записанное в десятичной системе исчисления (1 ≤ ci ≤ 1018).
Пожалуйста, не используйте спецификатор %lld для чтения или записи 64-х битовых чисел на С++, вместо него рекомендуется использовать потоки cin, cout, а также спецификатор %I64d.
Для каждого рецепта посчитайте, на какое минимальное простое число делится контрольное число в этом рецепте, и выведите это простое число в отдельной строке. Если это число окажется больше 100, выведите -1.
1
1
1
2 ? 1
2
4
2 3 5 7
4
2 ?0 11
2 ?1 13
2 0? 17
2 1? 19
3
2
23
2
1
1000000000000000000
1
16 ?????????????? 1
-1
В первом тесте подходит любой однозначный номер в двоичной системе исчисления. Банка всего одна и ее цена равна 1, число c тоже равно 1, контрольное число равна 2. Минимальный простой делитель числа 2 равен 2.
Во втором тесте есть 4 баночки с номерами от 0 до 3, и цены равны 2, 3, 5 и 7, соответственно — первые четыре простых числа. Во всех рецептах номера должны быть двухзначные. В первом рецепте вторая цифра обязательно 0, во втором — вторая цифра обязательно 1, в третьем варианте — первая цифра обязательно 0, в четвертом — первая цифра обязательно 1. Следовательно, контрольные числа получаются: в первом варианте 2 × 5 + 11 = 21 (минимальный простой делитель — 3); во втором варианте 3 × 7 + 13 = 44 (минимальный простой делитель — 2); в третьем варианте 2 × 3 + 17 = 23 (минимальный простой делитель — 23) и, наконец, в четвертом варианте 5 × 7 + 19 = 54 (минимальный простой делитель — 2).
В третьем тесте номер должен быть четырнадцатизначным числом в шестандцатиричной системе исчисления. Номер 0 (номер единственной баночки) подходит, контрольное число будет будет равна 1018 + 1. Минимальный простой делитель этого числа равен 101, вывести надо -1.
