| Codeforces Round 739 (Div. 3) |
|---|
| Закончено |
Несколько человек (чётное количество) встали в круг. Люди стоят по кругу равномерно. Они пронумерованы по часовой стрелке от $$$1$$$, начиная с некоторого из них. Каждый смотрит через центр круга на противоположного человека.
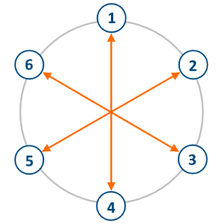 Пример круга для $$$6$$$ человек. Оранжевые стрелки указывают, кто на кого смотрит.
Пример круга для $$$6$$$ человек. Оранжевые стрелки указывают, кто на кого смотрит. Вы не знаете, сколько конкретно человек стоит в круге (но их точно чётное количество). Известно, что человек с номером $$$a$$$ смотрит на человека с номером $$$b$$$ (и, конечно, наоборот). На кого смотрит человек с номером $$$c$$$? Если для заданных $$$a$$$, $$$b$$$ и $$$c$$$ такого круга не существует, то выведите -1.
В первой строке записано одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следуют $$$t$$$ наборов входных данных.
Каждый набор входных данных состоит из одной строки, содержащей три различных целых числа $$$a$$$, $$$b$$$, $$$c$$$ ($$$1 \le a,b,c \le 10^8$$$).
Для каждого набора входных данных в отдельной строке выведите целое число $$$d$$$ — номер человека, на кого может смотреть человек $$$c$$$ в таком круге, что $$$a$$$ смотрит на $$$b$$$. Если существует несколько решений, выведите любое из них. Выведите $$$-1$$$, если не существует круга, удовлетворяющего заданным условиям.
7 6 2 4 2 3 1 2 4 10 5 3 4 1 3 2 2 5 4 4 3 2
8 -1 -1 -1 4 1 -1
В первом наборе входных данных можно составить круг из $$$8$$$ человек. Тогда человек с номером $$$6$$$ будет смотреть на человека с номером $$$2$$$, а человек с номером $$$8$$$ будет смотреть на человека с номером $$$4$$$.
Во втором наборе входных данных не существует круга, удовлетворяющего заданным условиям. Если люди с номерами $$$2$$$ и $$$3$$$ смотрят друг на друга и при этом являются соседями, то круг состоит из $$$2$$$ людей. Но тогда они должны иметь номера $$$1$$$ и $$$2$$$, что противоречит условию.
В третьем наборе входных данных единственный допустимый круг, в котором человек с номером $$$2$$$ смотрит на человека с номером $$$4$$$, состоит из $$$4$$$ человек. Таким образом, человека с номером $$$10$$$ не может быть в этом круге.
| Название |
|---|




