| Codeforces Global Round 16 |
|---|
| Закончено |
Деревом называется связный граф без циклов. В корневом дереве есть особая вершина, которая называется корнем. Родитель вершины $$$v$$$ (отличной от корня) — вершина перед $$$v$$$ на кратчайшем пути от корня до $$$v$$$. Дети вершины $$$v$$$ — все вершины, для которых $$$v$$$ является родителем.
Вершина называется листом, если у неё нет детей. Назовем вершину почкой, если выполняются три следующих условия:
- она не является корнем,
- у неё есть хотя бы один ребёнок, и
- все её дети — листья.
Вам дано корневое дерево из $$$n$$$ вершин. Вершина $$$1$$$ — корень. За одно действие вы можете выбрать любую почку со всеми её детьми (они являются листьями) и переподвесить её за любую другую вершину дерева. Таким действием вы удаляете ребро, соединяющее почку и родителя, и добавляете ребро между почкой и выбранной вершиной дерева. Эта выбранная вершина не может совпадать с выбранной почкой или быть одним из ее детей. Все дети почки остаются соединёнными с ней.
Какое минимальное количество листьев можно получить, если разрешается сделать любое количество вышеописанных действий (возможно, ни одного)?
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится единственное целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит единственное целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин в данном дереве.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \neq v$$$), которые означают, что есть в дереве есть ребро между вершинами $$$u$$$ и $$$v$$$.
Гарантируется, что данный граф является деревом.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно число — минимальное количество листьев, которое можно получить после нескольких (возможно нуля) действий.
5 7 1 2 1 3 1 4 2 5 2 6 4 7 6 1 2 1 3 2 4 2 5 3 6 2 1 2 7 7 3 1 5 1 3 4 6 4 7 2 1 6 2 1 2 3 4 5 3 4 3 6
2 2 1 2 1
В первом наборе входных данных дерево выглядит следующим образом:
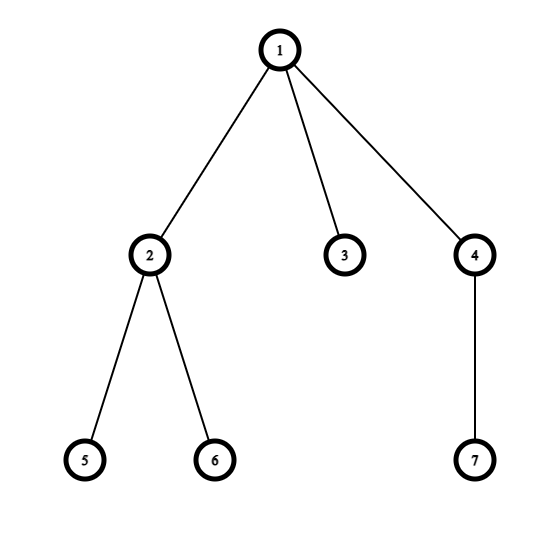
Сначала вы можете выбрать почку $$$4$$$ и переподвесить её за вершину $$$3$$$. После этого вы можете выбрать почку $$$2$$$ и переподвесить её за вершину $$$7$$$. В результате вы получите следующее дерево с $$$2$$$ листьями:
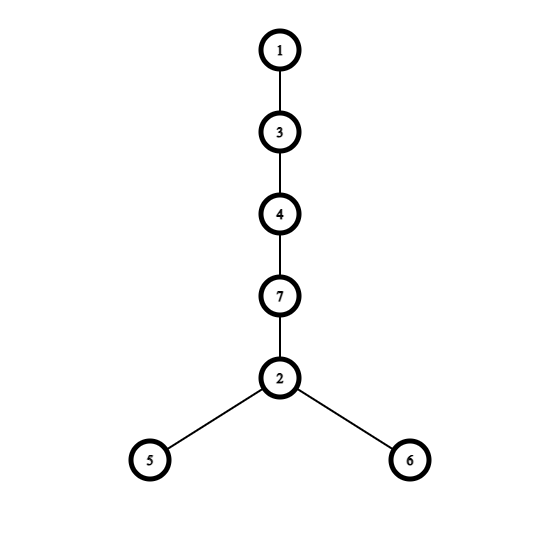
Можно доказать, что это минимальное количество листьев, которое можно получить.
Во втором наборе входных данных дерево выглядит следующим образом:
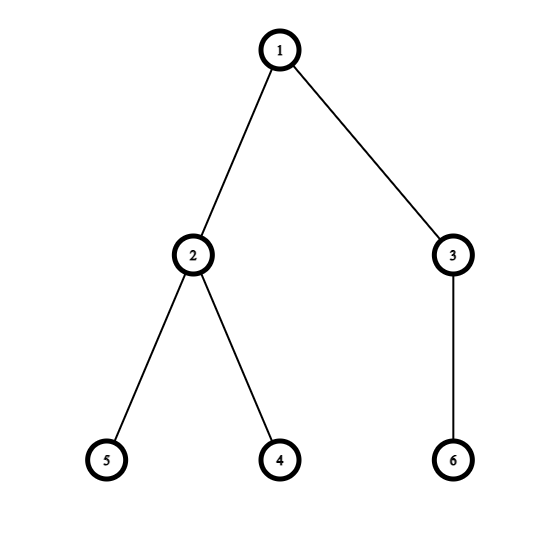
Вы можете выбрать почку $$$3$$$ и переподвесить её за вершину $$$5$$$. В результате вы получите следующее дерево с $$$2$$$ листьями:
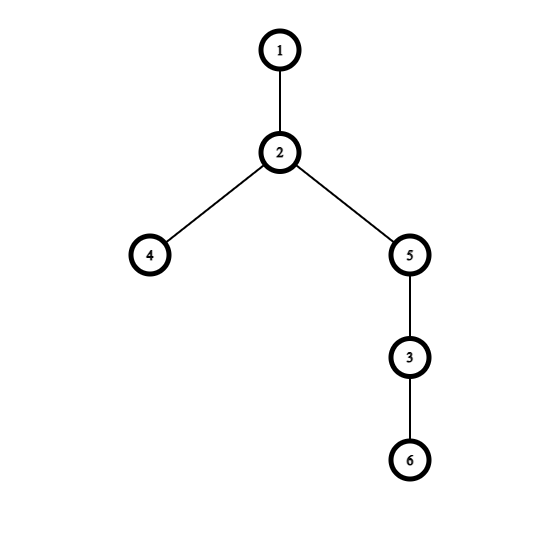
Можно доказать, что это минимальное количество листьев, которое можно получить.
| Название |
|---|




