| Технокубок 2022 - Отборочный Раунд 3 |
|---|
| Закончено |
Алиса и Боб — два браконьера, которые рубят лес.
Лес это набор (возможно пустой) деревьев. Дерево — это связный граф без циклов. Подвешенное дерево имеет специальную вершину — корень. Родителем вершины $$$v$$$ называется следующая вершина на кратчайшем пути от $$$v$$$ до корня. Детьми вершины $$$v$$$ называются вершины, для которых $$$v$$$ является родителем. Вершина называется листом, если у неё нет детей.
В этой задаче мы определим глубину вершины как количество вершин на простом пути от этой вершины до корня. Рангом дерева назовем минимальную глубину его листа.
Изначально дан непустой лес подвешенных деревьев. Алиса и Боб играют в игру на этом лесе. Они ходят по очереди, Алиса ходит первой. В начале каждого хода игрок выбирает дерево из леса. Далее игрок выбирает положительное целое число — глубину разреза, которая не превосходит ранга выбранного дерева. Затем игрок удаляет из дерева все вершины, чьи глубины меньше либо равны глубине разреза. Все остальные вершины разбиваются на набор подвешенных деревьев, корнем каждого становится вершина, имевшая наименьшую глубину в дереве до разреза. Все эти деревья добавляются в лес и игра продолжается.
Игрок проигрывает, если на момент начала его хода лес пуст.
Определите, может ли Алиса победить, если оба игрока играют оптимально.
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 5 \cdot 10^5$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
Первая строка набора входных данных содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 5 \cdot 10^5$$$) — суммарное количество вершин в деревьях изначального леса.
Вторая строка содержит $$$n$$$ целых чисел $$$p_1, p_2, \ldots, p_n$$$ ($$$0 \leq p_i \leq n$$$) — описание леса. Если $$$p_i = 0$$$, то $$$i$$$-я вершина дерева является корнем, иначе $$$p_i$$$ является родителем вершины $$$i$$$. Гарантируется, что $$$p$$$ задает корректный лес подвешенных деревьев.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$5 \cdot 10^5$$$.
Для каждого набора входных данных выведите «YES» (без кавычек), если Алиса может победить, иначе выведите «NO» (без кавычек). Вы можете выводить каждую букву в любом регистре.
4 4 0 1 0 3 7 0 1 2 0 4 5 6 4 0 1 1 2 7 0 1 1 2 2 3 3
NO YES NO YES
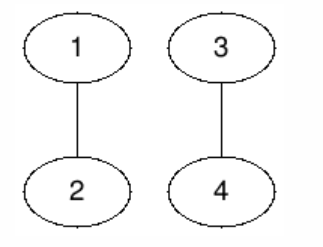
В первом наборе входных данных у Боба есть симметричная стратегия, поэтому Алиса выиграть не может.
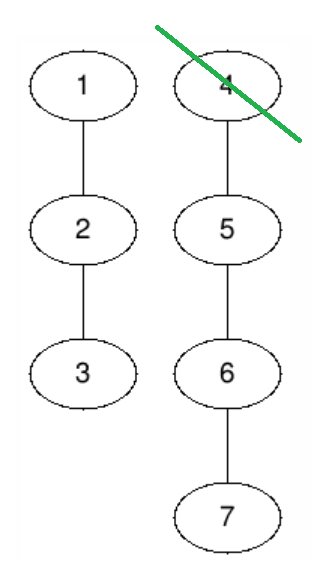
Во втором наборе Алиса может выбрать второе дерево и глубину разреза $$$1$$$, чтобы получить лес, где уже у нее есть симметричная стратегия.
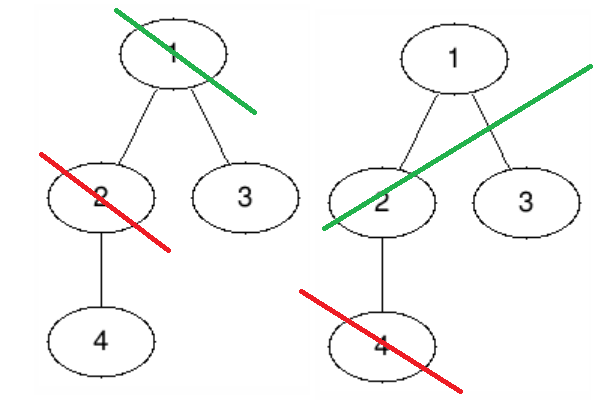
В третьем наборе ранг единственного дерева равен $$$2$$$, и оба возможных хода Алисы приводят к неудаче. В первом случае Боб может перейти к позиции с симметричной стратегией, а во втором сразу опустошить лес.
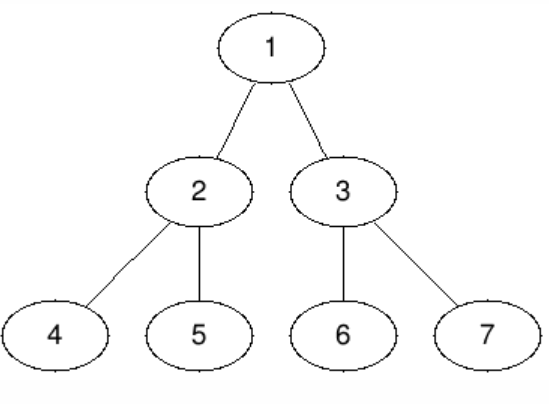
В четвертом наборе все листья единственного дерева имеют одинаковую глубину, поэтому Алиса может за один ход опустошить весь лес.
| Название |
|---|




