| Codeforces Round 746 (Div. 2) |
|---|
| Закончено |
Бакри столкнулся с задачей, но поскольку ему лень ее решать, он просит вашей помощи.
Вам дано дерево на $$$n$$$ вершинах, $$$i$$$-й вершине присвоено значение $$$a_i$$$ для каждого $$$i$$$ от $$$1$$$ до $$$n$$$. Напомним, что дерево на $$$n$$$ вершинах — это связный граф с $$$n-1$$$ ребрами.
Вы хотите удалить из дерева не менее $$$1$$$, но не более $$$k-1$$$ ребер так, чтобы выполнялось следующее условие:
Для каждой компоненты связности вычислим побитовое исключающего ИЛИ значений вершин в ней. Тогда, эти значения должны быть одинаковыми для всех компонент связности.
Возможно ли выполнить это условие?
Каждый тест содержит несколько наборов входных данных. Первая строка содержит количество наборов входных данных $$$t$$$ $$$(1 \leq t \leq 5 \cdot 10^4)$$$. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$k$$$ $$$(2 \leq k \leq n \leq 10^5)$$$.
Вторая строка каждого набора входных данных содержит $$$n$$$ целых чисел $$$a_1, a_2, ..., a_n$$$ $$$(1 \leq a_i \leq 10^9)$$$.
В $$$i$$$-й из следующих $$$n-1$$$ строк содержится два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i\neq v_i$$$), что означает, что между вершинами $$$u_i$$$ и $$$v_i$$$ есть ребро.
Гарантируется, что данный граф является деревом.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$.
Для каждого набора входных данных вы должны вывести одну строку. Если вы можете удалить ребра в соответствии с условиями, написанными выше, выведите «YES» (без кавычек). В противном случае выведите «NO» (без кавычек).
Вы можете вывести каждую букву «YES» и «NO» в любом регистре (верхнем или нижнем).
5 2 2 1 3 1 2 5 5 3 3 3 3 3 1 2 2 3 1 4 4 5 5 2 1 7 2 3 5 1 2 2 3 1 4 4 5 5 3 1 6 4 1 2 1 2 2 3 1 4 4 5 3 3 1 7 4 1 2 2 3
NO YES NO YES NO
Можно показать, что условие недостижимо для первого, третьего и пятого наборов входных данных.
Во втором наборе входных данных можно просто удалить все ребра. Останется $$$5$$$ компонент связности, каждая из которых содержит только одну вершину со значением $$$3$$$, поэтому побитовое ИЛИ для каждой из них будет $$$3$$$.
В четвертом случае дерево изображено ниже: 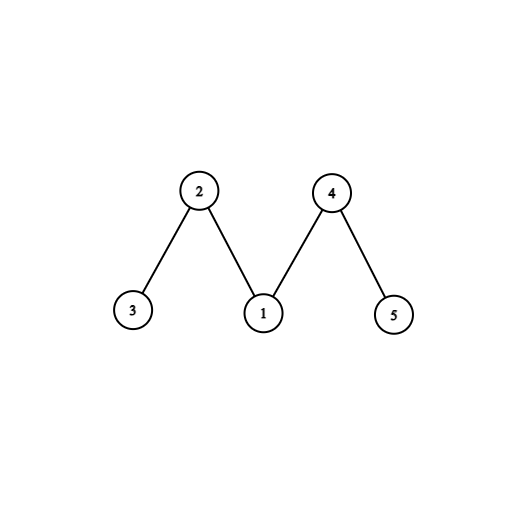 .
.
Вы можете удалить ребро $$$(4,5)$$$.
Побитовое ИЛИ первой компоненты будет равен $$$a_1 \oplus a_2 \oplus a_3 \oplus a_4 = 1 \oplus 6 \oplus 4 \oplus 1 = 2$$$ (где $$$\oplus$$$ обозначает побитовое ИЛИ).
Побитовое ИЛИ второй компоненты будет равно $$$a_5 = 2$$$.
| Название |
|---|




