| Codeforces Round 111 (Div. 2) |
|---|
| Закончено |
Дан связный взвешенный неориентированный граф без петель и кратных ребер.
Напоминаем, что остовным деревом графа называется ациклический связный подграф данного графа, в который входят все его вершины. Весом дерева называется сумма весов входящих в него ребер. Минимальным остовным деревом (MST) графа называется остовное дерево этого графа, имеющее минимальный возможный вес. Очевидно, что для любого связного графа минимальное остовное дерево существует, но, в общем случае, минимальное остовное дерево графа не единственно.
Ваша задача — для каждого ребра данного графа определить: либо оно входит в любое MST, либо оно входит хотя бы в одно MST, либо оно не входит ни в одно MST.
В первой строке даны два целых числа n и m (2 ≤ n ≤ 105, 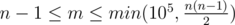 ) — количество вершин и ребер графа, соответственно. Далее следует m строк по три целых числа в каждой — описание ребер графа в формате «ai bi wi» (1 ≤ ai, bi ≤ n, 1 ≤ wi ≤ 106, ai ≠ bi), где ai и bi — номера вершин, которые соединяет i-е ребро, wi — вес ребра. Гарантируется, что граф связный, и не содержит петель и кратных ребер.
) — количество вершин и ребер графа, соответственно. Далее следует m строк по три целых числа в каждой — описание ребер графа в формате «ai bi wi» (1 ≤ ai, bi ≤ n, 1 ≤ wi ≤ 106, ai ≠ bi), где ai и bi — номера вершин, которые соединяет i-е ребро, wi — вес ребра. Гарантируется, что граф связный, и не содержит петель и кратных ребер.
Выведите m строк — ответы для всех ребер. Если i-е ребро входит в любое MST, выведите «any»; если i-е ребро входит хотя бы в одно MST, выведите «at least one»; если i-е ребро не входит ни в одно MST, выведите «none». Ответы для ребер выводите в том порядке, в котором ребра заданы во входных данных.
4 5
1 2 101
1 3 100
2 3 2
2 4 2
3 4 1
none
any
at least one
at least one
any
3 3
1 2 1
2 3 1
1 3 2
any
any
none
3 3
1 2 1
2 3 1
1 3 1
at least one
at least one
at least one
Во втором примере для данного графа MST единственно: оно содержит первые два ребра.
В третьем примере для данного графа любые два ребра образуют MST. Значит, любое ребро входит хотя бы в одно MST.
| Название |
|---|




