Дано дерево, состоящее из $$$n$$$ вершин. Напомним, что дерево — это неориентированный ацикличный граф. Корнем данного дерева является вершина $$$1$$$.
Требуется обработать $$$q$$$ запросов. В каждом запросе задается вершина дерева $$$v$$$ и целое число $$$k$$$.
Для обработки запроса можно удалять вершины из дерева в произвольном порядке, кроме корня и вершины $$$v$$$. Когда вершина удаляется, ее дети становятся детьми ее родителя. Требуется обработать запрос так, чтобы максимизировать значение $$$c(v) - m \cdot k$$$ (где $$$c(v)$$$ — это итоговое количество детей вершины $$$v$$$, а $$$m$$$ — это количество удаленных вершин). Выведите максимальное значение, которое можно получить.
Запросы независимые: изменения, произведенные над деревом при обработке запроса, не затрагивают другие запросы.
В первой строке записано одно число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
Затем следует $$$n-1$$$ строка, в $$$i$$$-й из них записаны два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le n$$$; $$$x_i \ne y_i$$$) — концы $$$i$$$-го ребра. Данные ребра образуют дерево.
В следующей строке записано одно целое $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — количество запросов.
Затем следуют $$$q$$$ строк, в $$$j$$$-й из них записаны два целых числа $$$v_j$$$ и $$$k_j$$$ ($$$1 \le v_j \le n$$$; $$$0 \le k_j \le 2 \cdot 10^5$$$) — параметры $$$j$$$-го запроса.
На каждый запрос выведите одно целое число — максимальное значение $$$c(v) - m \cdot k$$$, которое можно получить.
8 6 7 3 2 8 3 5 7 7 4 7 1 7 3 6 1 0 1 2 1 3 7 1 5 0 7 200000
5 2 1 4 0 4
Дерево в первом примере показано на следующем изображении:
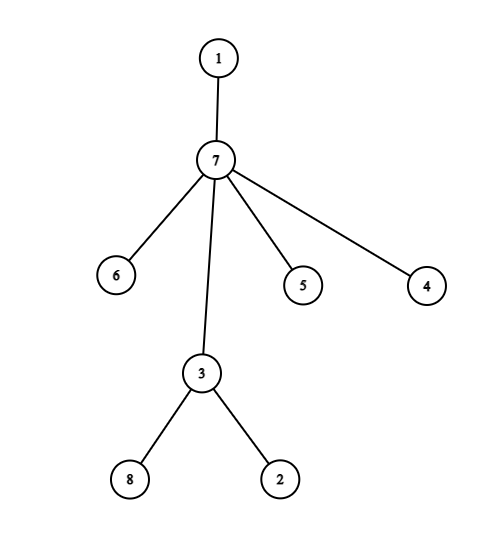
Ответы на запросы получаются следующим образом:
- $$$v=1,k=0$$$: можно удалить вершины $$$7$$$ и $$$3$$$, так, чтобы у вершины $$$1$$$ стало $$$5$$$ детей (вершины $$$2$$$, $$$4$$$, $$$5$$$, $$$6$$$ и $$$8$$$), и счет равен $$$5 - 2 \cdot 0 = 5$$$;
- $$$v=1,k=2$$$: можно удалить вершину $$$7$$$, так, чтобы у вершины $$$1$$$ стало $$$4$$$ ребенка (вершины $$$3$$$, $$$4$$$, $$$5$$$ и $$$6$$$), и счет равен $$$4 - 1 \cdot 2 = 2$$$.
- $$$v=1,k=3$$$: не надо удалять вершины; тогда у вершины $$$1$$$ станет один ребенок (вершина $$$7$$$), и счет равен $$$1 - 0 \cdot 3 = 1$$$;
- $$$v=7,k=1$$$: можно удалить вершину $$$3$$$, так, чтобы у вершины $$$7$$$ стало $$$5$$$ детей (вершины $$$2$$$, $$$4$$$, $$$5$$$, $$$6$$$ и $$$8$$$), и счет равен $$$5 - 1 \cdot 1 = 4$$$;
- $$$v=5,k=0$$$: что бы вы ни делали, у вершины $$$5$$$ не будет детей, поэтому счет равен $$$0$$$;
- $$$v=7,k=200000$$$: не надо удалять вершины; тогда у вершины $$$7$$$ станет $$$4$$$ ребенка (вершины $$$3$$$, $$$4$$$, $$$5$$$ и $$$6$$$), и счет равен $$$4 - 0 \cdot 200000 = 4$$$.
| Название |
|---|




