
На числовой прямой расположено $$$n$$$ роботов, $$$i$$$-й из них изначально занимает единичный отрезок $$$[x_i, x_i + 1]$$$. У каждого робота есть программа из $$$k$$$ команд, которые он выполняет по циклу. Команды пронумерованы от $$$1$$$ до $$$k$$$. Каждая команда описывается одним целым числом. Обозначим число, соответствующее $$$j$$$-й команде $$$i$$$-го робота, за $$$f_{i, j}$$$.
Изначальное положение роботов соответствует моменту времени $$$0$$$. В течение одной секунды с момента времени $$$t$$$ ($$$0 \le t$$$) до момента $$$t + 1$$$ происходит следующий процесс:
- Каждый робот выполняет $$$(t \bmod k + 1)$$$-ю команду из своего списка команд. Робот номер $$$i$$$ берет число $$$F = f_{i, (t \bmod k + 1)}$$$. Если это число отрицательное, робот пытается ехать влево с силой $$$|F|$$$, если положительное — пытается ехать вправо с силой $$$F$$$, иначе не делает ничего.
- Мысленно разобьем роботов на группы подряд идущих следующим алгоритмом:
- Изначально каждый робот принадлежит своей собственной группе.
- Просуммируем числа, соответствующие командам роботов, принадлежащих одной группе. Обратите внимание, что суммируются исходные числа, без взятия по модулю. Пусть сумма равна $$$S$$$. Скажем, что вся группа двигается вместе, и делает это с силой $$$S$$$, по тем же правилам, что и один робот. То есть, если $$$S$$$ отрицательно, пытается ехать влево с силой $$$|S|$$$, если $$$S$$$ положительно — вправо с силой $$$S$$$, иначе — не делает ничего.
- Если группа пытается двигаться в каком-то направлении, и в направлении движения касается другой группы, объединим их. Группа касается другой группы, если крайние роботы групп занимают соседние единичные отрезки.
- Продолжать процесс, пока группы не перестанут объединяться.
- Каждый робот перемещается на $$$1$$$ в направлении движения его группы, либо остается на месте, если группа не двигается. Но есть одно исключение.
- Исключение — если есть две группы роботов, разделенные ровно одним единичным отрезком, такие, что левая группа пытается двигаться вправо, а правая группа пытается двигаться влево. Обозначим сумму в левой группе за $$$S_l$$$, а в правой — за $$$S_r$$$. Если $$$|S_l| \le |S_r|$$$, перемещается только правая группа, иначе перемещается только левая группа.
- Обратите внимание, что роботы из одной группы не склеиваются друг с другом — в будущем они могут разъехаться. Разбиение на группы мысленное, и нужно только для того, чтобы понять, как роботы переместятся в течение одной секунды $$$[t, t + 1]$$$.
Иллюстрация процесса, происходящего в течение одной секунды:
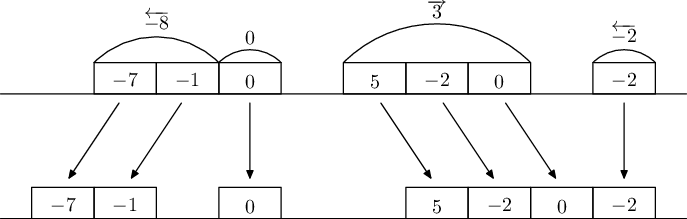
Прямоугольники обозначают роботов, числа в прямоугольниках соответствуют командам роботов. Дугами выделено итоговое разбиение на группы. Снизу нарисованы позиции роботов после перемещения. Из двух самых правых групп переместилась только левая, потому что эти две группы пытались двигаться навстречу друг другу и были разделены ровно одним единичным отрезком.
Смотрите примеры для лучшего понимания процесса.
Вам требуется ответить на несколько вопросов: где находится $$$a_i$$$-й робот в момент времени $$$t_i$$$.
В первой строке даны два целых числа $$$n$$$ и $$$k$$$ — количество роботов и количество команд в программе у одного робота ($$$1 \le n \le 100$$$, $$$1 \le k \le 50$$$).
В следующей строке даны $$$n$$$ целых чисел $$$x_i$$$ — позиции роботов в момент времени $$$0$$$ ($$$-10^9 \le x_1 < x_2 < \dots < x_n < 10^9$$$).
В следующих $$$n$$$ строках дано описание программ роботов. В $$$i$$$-й из этих строк находится $$$k$$$ целых чисел $$$f_{i, j}$$$ ($$$|f_{i, j}| \le 10^6$$$).
В следующей строке дано одно целое число $$$q$$$ — количество вопросов, на которые нужно ответить ($$$1 \le q \le 1000$$$).
В следующих $$$q$$$ строках дано по два целых числа $$$a_i$$$ и $$$t_i$$$, означающие, что вам нужно определить позицию $$$a_i$$$-го робота в момент времени $$$t_i$$$ ($$$1 \le a_i \le n$$$, $$$0 \le t_i \le 10^{18}$$$).
Для каждого вопроса выведите на новой строке одно целое число — координату левой границы единичного отрезка, который занимает $$$a_i$$$-й робот в момент времени $$$t_i$$$.
2 1 0 4 1 -1 8 1 0 2 0 1 1 2 1 1 2 2 2 1 3 2 3
0 4 1 3 1 2 1 2
2 1 0 4 2 -1 8 1 0 2 0 1 1 2 1 1 2 2 2 1 3 2 3
0 4 1 3 2 3 3 4
2 2 0 1 1 -1 -1 1 4 1 0 1 1 1 2 1 3
0 0 -1 0
1 3 0 3 -2 1 3 1 5 1 10 1 15
1 4 5
4 3 -8 -4 2 5 -1 3 0 1 -3 -4 2 -5 2 -1 -4 2 5 3 12 4 18 4 11 1 6 1 10
6 9 6 -8 -9
| Название |
|---|




