| Codeforces Global Round 17 |
|---|
| Закончено |
В последнее время Ли не мог заснуть, потому что ему снились кошмары. В одном из своих кошмаров (который был о несбалансированном глобал раунде) он решил дать отпор и предложить задачу ниже (которую вы должны решить), чтобы сбалансировать раунд, надеясь освободить его от кошмаров.
Непустой массив $$$b_1, b_2, \ldots, b_m$$$ называется хорошим, если существует $$$m$$$ целочисленных последовательностей, удовлетворяющих следующим свойствам:
- $$$i$$$-я последовательность состоит из $$$b_i$$$ последовательных целых чисел (например, если $$$b_i = 3$$$, то $$$i$$$-я последовательность может быть $$$(-1, 0, 1)$$$ или $$$(-5, -4, -3)$$$, но не $$$(0, -1, 1)$$$ или $$$(1, 2, 3, 4)$$$).
- Если сумма целых чисел в $$$i$$$-й последовательности равна $$$sum_i$$$, то мы хотим, чтобы $$$sum_1 + sum_2 + \ldots + sum_m$$$ было равно $$$0$$$.
Вам дан массив $$$a_1, a_2, \ldots, a_n$$$. У него есть $$$2^n - 1$$$ непустых подпоследовательностей. Найдите, сколько из них являются хорошими.
Поскольку это число может быть очень большим, выведите его по модулю $$$10^9 + 7$$$.
Массив $$$c$$$ является подпоследовательностью массива $$$d$$$, если $$$c$$$ может быть получен из $$$d$$$ путем удаления нескольких (возможно, нуля или всех) элементов.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — размер массива $$$a$$$.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le 10^9$$$) — элементы массива.
Выведите одно целое число — количество непустых хороших подпоследовательностей $$$a$$$, по модулю $$$10^9 + 7$$$.
4 2 2 4 7
10
10 12391240 103904 1000000000 4142834 12039 142035823 1032840 49932183 230194823 984293123
996
Для первого теста двумя примерами хороших подпоследовательностей являются $$$[2, 7]$$$ и $$$[2, 2, 4, 7]$$$:
Для $$$b = [2, 7]$$$ мы можем использовать $$$(-3, -4)$$$ в качестве первой последовательности и $$$(-2, -1, \ldots, 4)$$$ в качестве второй. Обратите внимание, что подпоследовательность $$$[2, 7]$$$ входит дважды в $$$[2, 2, 4, 7]$$$, поэтому мы должны считать ее дважды.
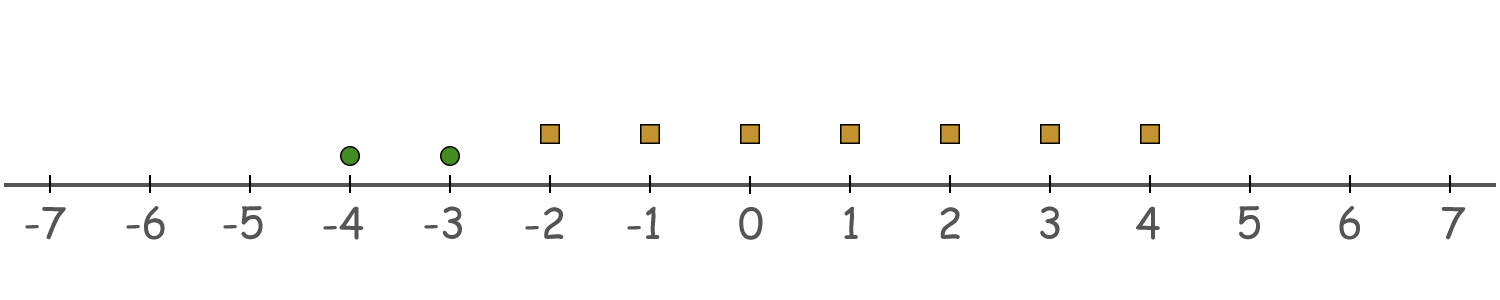 Зеленые круги обозначают $$$(-3, -4)$$$, а оранжевые квадраты - $$$(-2, -1, \ldots, 4)$$$.
Зеленые круги обозначают $$$(-3, -4)$$$, а оранжевые квадраты - $$$(-2, -1, \ldots, 4)$$$. Для $$$b = [2, 2, 4, 7]$$$ свойствам будут удовлетворять следующие последовательности: $$$(-1, 0)$$$, $$$(-3, -2)$$$, $$$(0, 1, 2, 3)$$$ и $$$(-3, -2, \ldots, 3)$$$.
| Название |
|---|




