| Codeforces Global Round 17 |
|---|
| Закончено |
После многих неудачных попыток, Маштали решил скопировать модифицировать задачу с AtCoder. Итак, вот его скопированная новая задача:
Дано дерево на $$$n$$$ вершинах, и некоторое непустое множество вершин прибито к земле.
Два игрока играют друг против друга на дереве. Они поочередно выполняют следующее действие:
- Удалить любое ребро из дерева, а затем удалить все компоненты связности, в которых нет прибитых вершин.
Игрок, который не сможет сделать ход, проигрывает (когда все ребра уже удалены).
Вам дано дерево, но не дано множество прибитых вершин. Ваша задача — определить для каждого $$$k$$$ победителя игры, если прибиты только вершины $$$1, 2, 3, \ldots, k$$$, и оба игрока играют оптимально.
Первая строка ввода содержит целое число $$$n$$$ — количество вершин ($$$1 \le n \le 3 \cdot 10^5$$$).
В $$$i$$$-й из следующих $$$n-1$$$ строк содержится два целых числа $$$u_i, v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \ne v_i$$$) — вершины $$$i$$$-го ребра. Гарантируется, что эти ребра образуют дерево.
Выведите строку длиной $$$n$$$. $$$i$$$-й символ должен быть '1', если первый игрок выиграл $$$i$$$-й сценарий, и '2' в противном случае.
5 1 2 2 3 2 4 4 5
11122
5 1 2 2 3 1 4 4 5
21122
6 1 2 2 4 5 1 6 3 3 2
111111
7 1 2 3 7 4 6 2 3 2 4 1 5
2212222
Ниже вы можете увидеть дерево с первого примера:
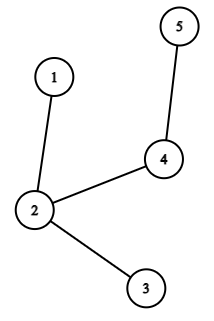
Если $$$k = 1$$$, то первый игрок может разрезать ребро $$$(1, 2)$$$.
Если $$$k = 2$$$ или $$$k = 3$$$, то первый игрок может перерезать ребро $$$(2, 4)$$$, после чего останутся только ребра $$$(1, 2)$$$ и $$$(2, 3)$$$. После хода второго игрока у первого игрока останется только одно ребро для разрезания. Поэтому первый игрок выигрывает.
| Название |
|---|




