| Codeforces Round 763 (Div. 2) |
|---|
| Закончено |
Дано бинарное дерево из $$$n$$$ вершин. Вершины дерева пронумерованы от $$$1$$$ до $$$n$$$, корень дерева имеет номер $$$1$$$. Каждая вершина может не иметь детей, иметь только правого или только левого ребенка, или иметь двух детей. Для удобства обозначим за $$$l_u$$$ и $$$r_u$$$ левого и правого ребенка вершины $$$u$$$ соответственно, при этом $$$l_u = 0$$$, если у $$$u$$$ нет левого ребенка, и $$$r_u = 0$$$, если у $$$u$$$ нет правого ребенка.
В каждой вершине дерева записана некоторая строка, изначально состоящая из одного символа $$$c_u$$$. Определим строковое представление дерева как конкатенацию всех строк, записанных в вершинах, в порядке центрированного обхода. Формально, пусть $$$f(u)$$$ — строковое представление поддерева с корнем в вершине $$$u$$$. $$$f(u)$$$ определена так: $$$$$$ f(u) = \begin{cases} \texttt{<пустая строка>,} & \text{если }u = 0; \\ f(l_u) + c_u + f(r_u) & \text{иначе}, \end{cases} $$$$$$ где $$$+$$$ обозначает строковую конкатенацию.
Представление всего дерева это $$$f(1)$$$.
Для каждой вершины мы можем продублировать строку, записанную в ней, не более одного раза, а именно, заменить $$$c_u$$$ на $$$c_u + c_u$$$. Эта операция возможна только если $$$u$$$ — корень дерева, или строка, записанная в родителе этой вершины уже продублирована.
Вам дано дерево и целое число $$$k$$$. Какое лексикографически минимальное строковое представление дерево может иметь, если мы можем продублировать строку в не более чем $$$k$$$ вершинах?
Строка $$$a$$$ лексикографически меньше строки $$$b$$$, если и только если выполняется один из следующих пунктов:
- $$$a$$$ — префикс $$$b$$$, но $$$a \ne b$$$;
- в первой позиции, где $$$a$$$ и $$$b$$$ различны, в строке $$$a$$$ находится буква, которая встречается в алфавите раньше, чем соответствующая буква в $$$b$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le k \le n \le 2 \cdot 10^5$$$).
Вторая строка содержит строку $$$c$$$, состоящую из $$$n$$$ маленьких букв латинского алфавита, где $$$c_i$$$ — строка, записанная в вершине $$$i$$$ изначально, $$$1 \le i \le n$$$. Обратите внимание, что данная строка $$$c$$$ не является начальным строковым представлением дерева.
$$$i$$$-я из следующих $$$n$$$ строк содержит два целых числа $$$l_i$$$ и $$$r_i$$$ ($$$0 \le l_i, r_i \le n$$$). Если у $$$i$$$-й вершины нет левого ребенка, $$$l_i = 0$$$, и если у $$$i$$$-й вершины нет правого ребенка, $$$r_i = 0$$$.
Гарантируется, что данные значения описывают корректное бинарное дерево с корнем в $$$1$$$.
Выведите одну строку, содержащую лексикографически минимальное строковое представление, которое может иметь дерево после не более чем в $$$k$$$ вершинах строка будет продублирована.
4 3 abab 2 3 0 0 0 4 0 0
baaaab
8 2 kadracyn 2 5 3 4 0 0 0 0 6 8 0 7 0 0 0 0
daarkkcyan
8 3 kdaracyn 2 5 0 3 0 4 0 0 6 8 0 7 0 0 0 0
darkcyan
Рисунке ниже иллюстрируют примеры. Число в вершине обозначает номер вершины, а строка в нижнем индексе — строку, написанную в вершине. Справа находится строковое представление дерева, где каждая буква имеет цвет соответствующей вершине дерева.
Ниже находится дерево для первого примера. Мы продублировали строки в вершинах $$$1$$$ и $$$3$$$. Строку в вершине $$$2$$$ не нужно дублировать, так как в таком случае представление будет «bbaaab», что лексикографически больше, чем «baaaab».
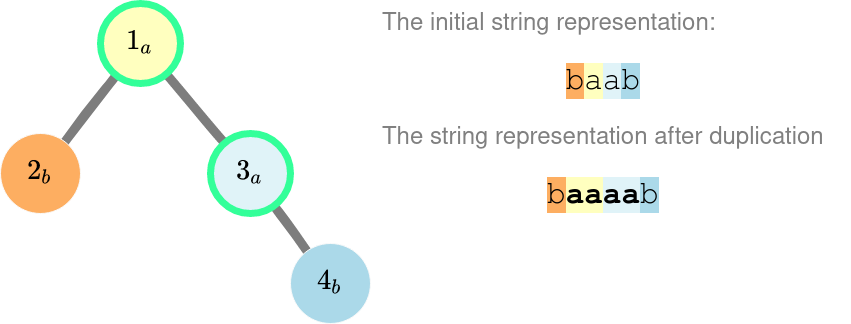
Во втором примере можно продублировать строки в вершинах $$$1$$$ и $$$2$$$. Обратите внимание, что если продублировать только строку в корне, то представление будет хуже, чем у изначального дерева.
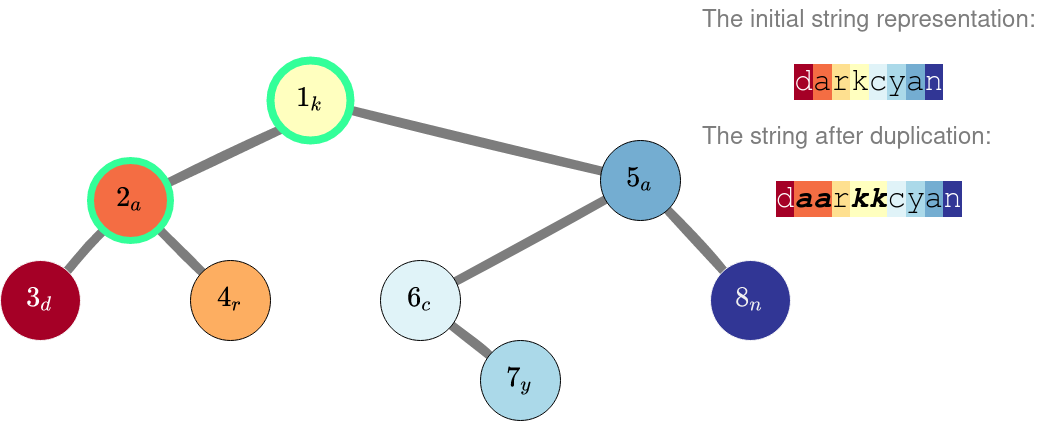
В третьем примере не нужно ничего дублировать. Даже если мы продублируем строку в вершине $$$3$$$, мы будем обязаны также продублировать строку в вершине $$$2$$$, что сделает результат хуже.
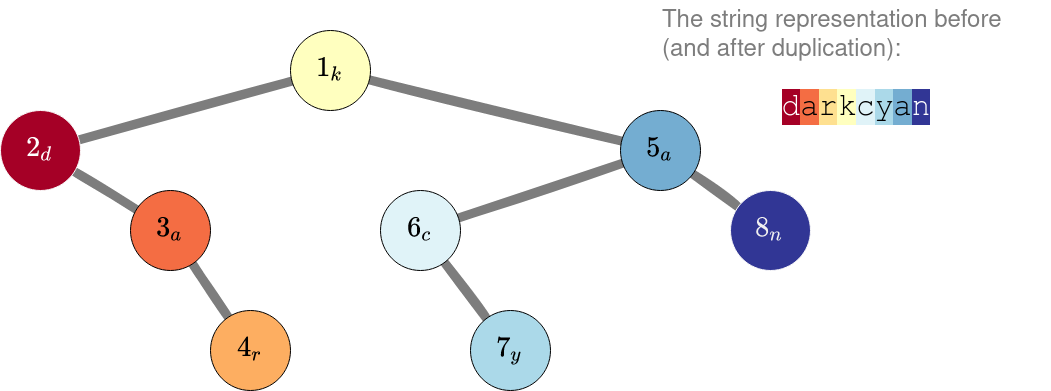
Нет способа получить строку «darkkcyan» из дерева с начальным представлением «darkcyan» :(.
| Название |
|---|




