| Codeforces Round 764 (Div. 3) |
|---|
| Закончено |
В последнее время Влад увлёкся остовными деревьями, так что его друзья не долго думая подарили ему на день рождения связный взвешенный неориентированный граф из $$$n$$$ вершин и $$$m$$$ рёбер.
Влад определил орность остовного дерева как побитовое ИЛИ всех его весов и теперь его интересует, какова минимальная возможная орность, которой можно добиться, выбрав некоторое остовное дерево. Остовное дерево — связный подграф данного графа, не содержащий циклов.
Иными словами вы хотите оставить $$$n-1$$$ ребро, так чтобы граф остался связным и побитовое ИЛИ весов рёбер было как можно меньше. Вы должны найти само побитовое ИЛИ.
В первой строке входных данных записано целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных в тесте.
Перед каждым набором в тесте записана пустая строка.
Далее следуют два числа $$$n$$$ и $$$m$$$ ($$$3 \le n \le 2 \cdot 10^5, n - 1 \le m \le 2 \cdot 10^5$$$) — количество вершин и рёбер графа, соответственно.
Следующие $$$m$$$ строк содержат описание рёбер. Строка $$$i$$$ содержит три числа $$$v_i$$$, $$$u_i$$$ и $$$w_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$1 \le w_i \le 10^9$$$, $$$v_i \neq u_i$$$) — вершины, которые соединяет ребро, и его вес.
Гарантируется, что сумма $$$m$$$ и сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$ и каждый тест содержит связный граф.
Выведите $$$t$$$ строк, каждая из которых содержит ответ на соответствующий набор входных данных — минимальную возможную орность остовного дерева.
33 31 2 12 3 21 3 25 74 2 72 5 83 4 23 2 12 4 24 1 21 2 23 41 2 12 3 21 3 33 1 4
2 10 3
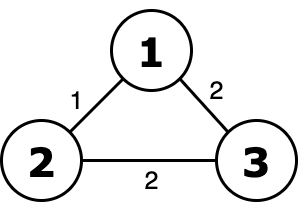 Изначальный граф из первого примера.
Изначальный граф из первого примера. 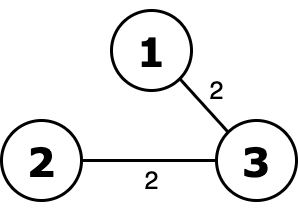 Орность такого дерева равна 2 or 2 = 2 и является оптимальной.
Орность такого дерева равна 2 or 2 = 2 и является оптимальной. 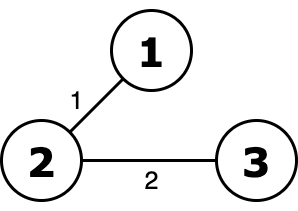 Оставив ребро веса $$$1$$$ мы получим орность 1 or 2 = 3.
Оставив ребро веса $$$1$$$ мы получим орность 1 or 2 = 3.
| Название |
|---|




