| Codeforces Round 771 (Div. 2) |
|---|
| Закончено |
Вы нашли картину на холсте размером $$$n \times m$$$. Холст можно представить в виде сетки с $$$n$$$ строками и $$$m$$$ столбцами. Каждая клетка покрашена в какой-то цвет. Клетка $$$(i, j)$$$ имеет цвет $$$c_{i,j}$$$.
Рядом с картиной вы также нашли кисть в форме квадрата $$$2 \times 2$$$, поэтому холст был покрашен следующим образом. Изначально никакая клетка не была покрашена. Затем следующая операция покраски была выполнена некоторое количество раз:
- Выбрать два целых числа $$$i$$$ и $$$j$$$ ($$$1 \le i < n$$$, $$$1 \le j < m$$$) и некоторый цвет $$$k$$$ ($$$1 \le k \le nm$$$).
- Покрасить клетки $$$(i, j)$$$, $$$(i + 1, j)$$$, $$$(i, j + 1)$$$, $$$(i + 1, j + 1)$$$ в цвет $$$k$$$.
Каждая клетка должна быть покрашена хотя бы один раз. Клетка может быть покрашена несколько раз. В этом случае её итоговый цвет будет равен последнему.
Найдите некоторую последовательность из не более $$$nm$$$ операций, позволяющую получить картину, которую вы нашли, или определите, что это невозможно.
Первая строка входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n, m \le 1000$$$) — размеры холста.
В $$$i$$$-й из следующих $$$n$$$ строк входных данных содержатся $$$m$$$ целых чисел. $$$j$$$-е из них равно $$$a_{i,j}$$$ ($$$1 \le a_{i,j} \le nm$$$) — цвет клетки $$$(i, j)$$$.
Если решения не существует, выведите единственное число $$$-1$$$.
Иначе, на первой строке, выведите одно целое число $$$q$$$ ($$$1 \le q \le nm$$$) — количество операций.
Далее выведите сами операции по порядку. В $$$k$$$-й из следующих $$$q$$$ строк, выведите три целых числа $$$i$$$, $$$j$$$, $$$c$$$ ($$$1 \le i < n$$$, $$$1 \le j < m$$$, $$$1 \le c \le nm$$$) — описание $$$k$$$-й операции.
Если существует несколько решений, выведите любое.
4 4 5 5 3 3 1 1 5 3 2 2 5 4 2 2 4 4
6 1 3 3 3 3 4 2 2 5 1 1 5 2 1 1 3 1 2
3 4 1 1 1 1 2 2 3 1 2 2 1 1
-1
В первом наборе входных данных решение не единственно. Здесь представлено одно из них:
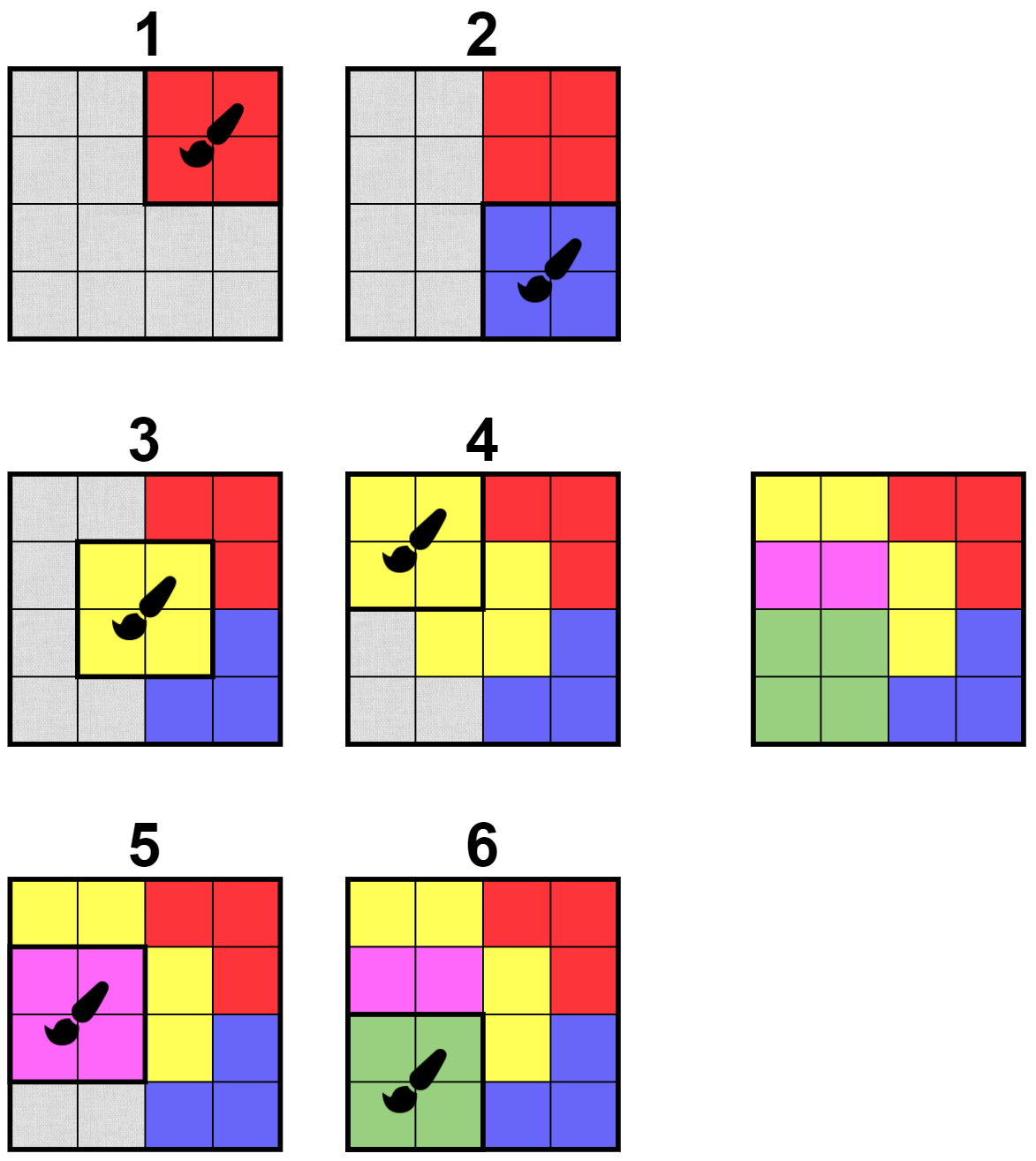
Во втором наборе входных данных не существует способа получить данную картину, поэтому ответ $$$-1$$$.
| Название |
|---|




