| VK Cup 2012 Раунд 3 |
|---|
| Закончено |
У Поликарпа есть очень много работ. Каждая работа характеризуется тремя целыми числами li, ri и ti. Тройка (li, ri, ti) означает, что для выполнения работы i нужно выбрать целое число si (li ≤ si; si + ti - 1 ≤ ri), тогда работа будет выполняться непрерывно ti единиц времени, начиная с момента времени si и до момента времени si + ti - 1, включительно. Иными словами, работа выполняется в течение непрерывного отрезка времени продолжительностью ti, должна быть начата не раньше li, а закончена не позже ri.
Работы Поликарпа обладают удивительным свойством: для любых работ j, k (при j < k) lj < lk и rj < rk.
Пусть имеется упорядоченное множество работ A, содержащее |A| работ. Будем считать, что aj = (lj, rj, tj) (1 ≤ j ≤ |A|). Также будем считать, что работы упорядочены по возрастанию lj с увеличением номера.
Рассмотрим следующую рекурсивную функцию f, аргументом которой является упорядоченное множество работ A, а результатом является целое число. Функция f(A) определяется жадным алгоритмом, которые описан ниже на псевдоязыке программирования.
- Шаг 1.
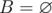 , ans = 0.
, ans = 0. - Шаг 2. Рассматриваем все работы в порядке увеличения их номера в множестве A. Заведем счетчик текущей работы, i = 0.
- Шаг 3. Переходим к следующей работе: i = i + 1. Если i > |A|, то перейти к шагу 8.
- Шаг 4. Если можно выполнить работу в момент времени si = max(ans + 1, li), то выполнить работу i: si = max(ans + 1, li), ans = si + ti - 1,
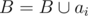 . Перейти к следующей работе (шаг 3).
. Перейти к следующей работе (шаг 3). - Шаг 5. Иначе, найти такую работу
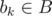 , что, во-первых, работу ai можно выполнить в момент времени si = max
, что, во-первых, работу ai можно выполнить в момент времени si = max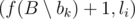 , во-вторых, значение
, во-вторых, значение 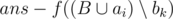 положительно и принимает максимальное значение среди всех bk, удовлетворяющих первому условию. Если в качестве bk можно выбрать несколько работ, выбрать ту, у которой номер в множестве A наибольший.
положительно и принимает максимальное значение среди всех bk, удовлетворяющих первому условию. Если в качестве bk можно выбрать несколько работ, выбрать ту, у которой номер в множестве A наибольший. - Шаг 6. Если удалось выбрать работу bk, то
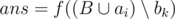 ,
, 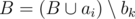 . Перейти к следующей работе (шаг 3).
. Перейти к следующей работе (шаг 3). - Шаг 7. Если не удалось выбрать работу bk, то пропустить работу i. Перейти к следующей работе (шаг 3).
- Шаг 8. Выдать ans в качестве результата работы f(A).
Поликарп запутался во всех этих формулах и определениях, поэтому он попросил вас промоделировать работу функции f, вычислите значение f(A).
В первой строке входных данных записано единственное целое число n (1 ≤ n ≤ 105) — количество работ в множестве A.
Далее в n строках описаны сами работы. В i-й строке записано три целых числа через пробел li, ri, ti (1 ≤ li ≤ ri ≤ 109, 1 ≤ ti ≤ ri - li + 1) — описание i-й работы.
Гарантируется, что для любых работ j, k (при условии j < k) верно, что lj < lk и rj < rk.
Для каждой работы i выведите одно целое число — результат обработки работы i на i-ой итерации цикла (шага 3) в функции f(A). В i-й строке выведите:
- 0 — если работу i получилось добавить на шаге 4.
- -1 — если работу i не получилось ни добавить, ни заменить (шаг 7).
- resi (1 ≤ resi ≤ n) — если работу получилось заменить (шаг 6): resi равно номеру работы (в множестве A), которую можно выбрать в качестве bk и заменить на работу ai.
5
1 8 5
2 9 3
3 10 3
8 11 4
11 12 2
0 0 1 0 -1
13
1 8 5
2 9 4
3 10 1
4 11 3
8 12 5
9 13 5
10 14 5
11 15 1
12 16 1
13 17 1
14 18 3
15 19 3
16 20 2
0 0 0 2 -1 -1 0 0 0 0 7 0 12
| Название |
|---|




