D. Взвесьте дерево
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Вам дано дерево из $$$n$$$ вершин, пронумерованных от $$$1$$$ до $$$n$$$. Деревом называется связный неориентированный граф без циклов.

Для всех $$$i=1,2, \ldots, n$$$ обозначим за $$$w_i$$$ вес $$$i$$$-й вершины. Вершина называется хорошей, если ее вес равен сумме весов всех ее соседей.

Изначально веса в вершинах не определены. Выберете для каждой вершины положительный целочисленный вес так, чтобы количество хороших вершин в дереве было максимально возможным. Если есть несколько способов сделать это, вам нужно найти такой, который минимизирует сумму весов всех вершин в дереве.

Входные данные

Первая строка содержит одно целое число $$$n$$$ ($$$2\le n\le 2\cdot 10^5$$$) — количество вершин в дереве.

Далее следует $$$n−1$$$ строка. Каждая из этих строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1\le u,v\le n$$$), обозначающие ребро между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что ребра образуют дерево.

Выходные данные

В первой строке выведите два целых числа: максимальное количество хороших вершин и минимально возможный суммарный вес вершин при этом.

Во второй строке выведите $$$n$$$ целых чисел $$$w_1, w_2, \ldots, w_n$$$ ($$$1\le w_i\le 10^9$$$) — веса вершин. Можно показать, что существует оптимальное решение, удовлетворяющее данным ограничениям.

Если существует несколько решений, выведите любое из них.

Примеры
Входные данные
4
1 2
2 3
2 4
Выходные данные
3 4
1 1 1 1
Входные данные
3
1 2
1 3
Выходные данные
2 3
1 1 1
Входные данные
2
1 2
Выходные данные
2 2
1 1
Входные данные
9
3 4
7 6
2 1
8 3
5 6
1 8
8 6
9 6
Выходные данные
6 11
1 1 1 1 1 1 1 3 1
Примечание

Ниже изображено дерево из первого примера:

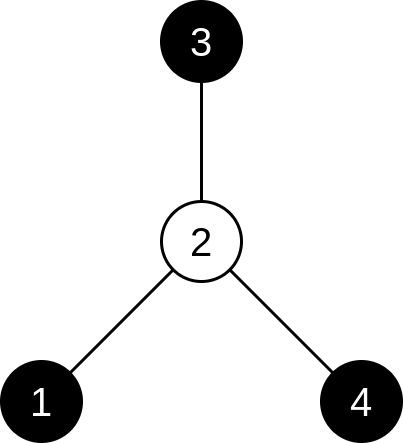
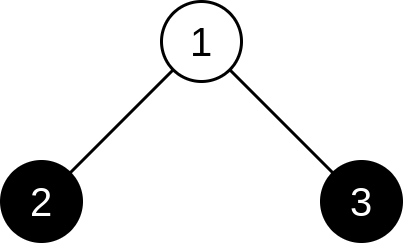
В этом случае, если вы выберете для каждый вершины вес $$$1$$$, то хорошими вершинами будут вершины (покрашены черным) $$$1$$$, $$$3$$$ и $$$4$$$. Невозможно выбрать такие веса, чтобы все вершины были хорошими. Минимально возможная сумма весов равна $$$1+1+1+1=4$$$, меньшая сумма недостижима, так как вершины обязаны иметь положительный вес.

Ниже изображено дерево из второго примера:

В этом случае, если вы выберете для каждой вершины вес $$$1$$$, то хорошими вершинами будут вершины (покрашены черным) $$$2$$$ и $$$3$$$. Можно показать, что это оптимальное решение.