| Codeforces Round 113 (Div. 2) |
|---|
| Закончено |
Медианой в массиве длины n называется элемент, который после сортировки элементов по неубыванию будет стоять на позиции номер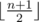 
(элементы массива нумеруются начиная с 1). Медианой массива (2, 6, 1, 2, 3) является число 2, а медианой массива (0, 96, 17, 23) — число 17.
Под выражением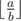 
понимается целая часть от деления числа a на число b.
Однажды Вася показал Пете массив из n натуральных чисел и предложил найти медиану этого массива. Петя, даже не взглянув на числа, ответил, что она равна x. Петя очень честный мальчик, поэтому он решил добавить к заданному массиву несколько чисел таким образом, чтобы медиана получившегося массива стала равна x.
Петя может добавлять в массив любые целые числа от 1 до 105, в том числе и одинаковые. Разумеется, разрешается ничего не добавлять в массив. Если число добавляется несколько раз, то в ответе оно учитывается такое же количество раз. Исходные числа массива запрещено удалять либо заменять.
Пока Петя отвлекает Васю, вы должны найти минимальное количество чисел, которые ему потребуются.
В первой строке входных данных записаны два разделенных пробелом целых числа n и x (1 ≤ n ≤ 500, 1 ≤ x ≤ 105) — длина исходного массива и требуемое значение медианы. Во второй строке записаны n чисел через пробел — исходный массив. Элементы массива — целые числа от 1 до 105. Элементы массива не обязательно различны.
Выведите единственное целое число — минимальное количество чисел, которое нужно добавить Пете в массив, чтобы его медиана стала равна x.
3 10
10 20 30
1
3 4
1 2 3
4
В первом примере в массив (10, 20, 30) достаточно добавить число 9. В получившемся массиве (9, 10, 20, 30) медианой будет элемент на позиции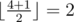 
, то есть 10.
Во втором примере в массив нужно добавить числа 4, 5, 5, 5. В получившемся массиве медиана равна 4.
