| Codeforces Round 783 (Div. 1) |
|---|
| Закончено |
Дана доска, состоящая из $$$n$$$ строк и $$$n$$$ столбцов, пронумерованных от $$$1$$$ до $$$n$$$. Пересечение $$$a$$$-й строки и $$$b$$$-го столбца обозначим за $$$(a, b)$$$.
Полуферзь может атаковать клетки, стоящие в той же строке, том же столбце и на той же диагонали, что и он. Более формально, полуферзь, стоящий в $$$(a, b)$$$ может атаковать клетку $$$(c, d)$$$, если $$$a=c$$$, или $$$b=d$$$, или $$$a-b=c-d$$$.
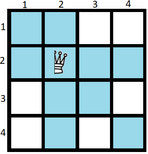 Голубые клетки находятся под атакой.
Голубые клетки находятся под атакой. Какое минимальное количество полуферзей нужно разместить на доске, чтобы каждая клетка была атакована хотя бы одним полуферзем?
Выведите оптимальное решение.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 10^5$$$) — размер доски.
В первой строке выведите одно целое число $$$k$$$ — минимальное количество полуферзей.
В каждой из следующих $$$k$$$ строках выведите два целых числа $$$a_i$$$, $$$b_i$$$ ($$$1 \le a_i, b_i \le n$$$) — местоположение $$$i$$$-го полуферзя.
Если существует несколько решений, выведите любое.
1
1 1 1
2
1 1 1
3
2 1 1 1 2
Пример $$$1$$$: одного полуферзя достаточно. Заметьте: полуферзь, стоящий в $$$(1, 1)$$$, атакует $$$(1, 1)$$$.
Пример $$$2$$$: одного полуферзя также достаточно. $$$(1, 2)$$$ и $$$(2, 1)$$$ — неверные решения, поскольку полуферзь, стоящий в $$$(1, 2)$$$, не атакует клетку $$$(2, 1)$$$, и наоборот. $$$(2, 2)$$$ также верное решение.
Пример $$$3$$$: невозможно покрыть доску одним полуферзем. Существует несколько решений для $$$2$$$-х полуферзей, вы можете вывести любое из них.
| Название |
|---|




