| Codeforces Round 114 (Div. 1) |
|---|
| Закончено |
В некоторой стране живут волшебники. Они любят заключать странные пари.
Два волшебника нарисовали ациклический ориентированный граф с n вершинами и m ребрами (вершины графа пронумерованы от 1 до n). Назовем истоком вершину, в которую не входит ни одного ребра, а стоком — вершину, из которой не выходит ни одного ребра. Заметим, что вершина может быть стоком и истоком одновременно. В графе волшебников количество стоков и истоков совпадает.
Волшебники занумеровали истоки в порядке увеличения номера вершины от 1 до k. Cтоки занумерованы от 1 до k аналогичным способом.
Для заключения пари, они, как настоящие волшебники, применяют заклинание, которое выбирает набор из k путей из всех истоков в стоки, причем так, что никакие два пути не пересекаются по вершинам. В таком случае в каждый сток ведет путь из ровно одного истока. Пусть в i-ый сток ведет путь из ai истока. Тогда назовем пару (i, j) инверсией, если i < j и ai > aj. Если количество инверсий среди всевозможных пар (i, j), таких что (1 ≤ i < j ≤ k), четно, то выиграл первый волшебник (второй отдает ему 1 волшебную монету). Иначе выиграл второй волшебник (он получает 1 волшебную монету от первого).
Наших волшебников охватил безумный азарт, поэтому они выбирали новые пути снова и снова так долго, что в итоге получили ровно по одному разу все возможные наборы путей. Наборы непересекающихся по вершинам путей считаются различными, если существует ребро, принадлежащее какому-то пути одного набора и не принадлежащее никакому пути другого набора. Для проверки своих записей они просят вас посчитать суммарный выигрыш первого игрока на этих наборах путей по модулю простого числа p.
В первой строке входного файла записано через пробел три целых числа n, m, p (1 ≤ n ≤ 600, 0 ≤ m ≤ 105, 2 ≤ p ≤ 109 + 7). Гарантируется, что p — простое.
В следующих m строках заданы ребра графа. В каждой строке находится пара целых чисел, разделенных пробелом, ai bi — ребро из вершины ai в вершину bi. Гарантируется, что граф ациклический и что в графе одинаковое число стоков и истоков. Обратите внимание, в графе могут быть кратные ребра.
Выведите ответ на задачу — суммарный выигрыш первого игрока по модулю простого числа p. Обратите внимание, что выигрыш может быть отрицательным, но остаток по модулю должен быть неотрицательным (см. пример).
4 2 1000003
1 3
2 4
1
4 2 1000003
4 1
3 2
1000002
4 4 1000003
2 1
2 4
3 1
3 4
0
6 5 1000003
1 4
1 5
1 6
2 6
3 6
0
5 2 1000003
5 1
3 4
1
В первом примере существует ровно 1 набор путей —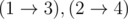 
. Число инверсий — 0, что является четным числом. Поэтому первый волшебник получает 1 монету.
Во втором примере существует ровно 1 набор путей —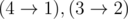 
. Существует ровно одна инверсия. Поэтому первый получает -1 монету. 
.
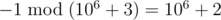В третьем примере существует два набора путей, которые учитываются с разными знаками.
В четвертом примере наборов путей вообще не существует.
В пятом примере есть три истока — вершины с номерами (2, 3, 5) и три стока — вершины с номерами (1, 2, 4). Для единственного набора путей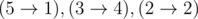 
существует 2 инверсии, то есть их число четно.
